题目内容
【题目】如图,正四面体![]() 的顶点
的顶点![]() 、
、![]() 、
、![]() 分别在两两垂直的三条射线
分别在两两垂直的三条射线![]() ,
, ![]() ,
, ![]() 上,则在下列命题中,错误的是( )
上,则在下列命题中,错误的是( )
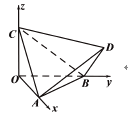
A. ![]() 是正三棱锥
是正三棱锥
B. 直线![]() 与平面
与平面![]() 相交
相交
C. 直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]()
D. 异面直线![]() 和
和![]() 所成角是
所成角是![]()
【答案】C
【解析】①如图ABCD为正四面体,
∴△ABC为等边三角形,
又∵OA、OB、OC两两垂直,
∴OA⊥面OBC,∴OA⊥BC,
过O作底面ABC的垂线,垂足为N,
连接AN交BC于M,
由三垂线定理可知BC⊥AM,
∴M为BC中点,
同理可证,连接CN交AB于P,则P为AB中点,
∴N为底面△ABC中心,
∴O﹣ABC是正三棱锥,故A正确.
②将正四面体ABCD放入正方体中,如图所示,显然OB与平面ACD不平行.
则B正确,

③由上图知:直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ,则C错误
,则C错误
④异面直线![]() 和
和![]() 所成角是
所成角是![]() ,故D正确.
,故D正确.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目