Question

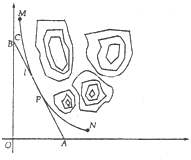
【题目】某山区外围有两条相互垂直的直线型公路，为进一步改善山区的交通现状，计划修建一条连接两条公路和山区边界的直线型公路．记两条相互垂直的公路为，山区边界曲线为．计划修建的公路为，如图所示，为的两个端点，测得点到的距离分别为5千米和40千米，点到的距离分别为20千米和2．5千米，以所在直线分别为轴，建立平面直角坐标系．假设曲线符合函数（其中为常数）模型．

（1）求的值；

（2）设公路与曲线相切于点，的横坐标为．

①请写出公路长度的函数解析式，并写出其定义域；

②当为何值时，公路的长度最短？求出最短长度．

Answer 1

【答案】（1）；（2）①；②当时，公路的长度最短，最短长度为千米．

【解析】

试题分析：（1）由题意得分别为

；（2）①由（1）知 ，求导得

；；

②设，令，利用导数工具可得：当时，函数有极小值，也是最小值，所以，此时．

试题解析：

（1）由题意知，点的坐标分别为．

将其分别代入，得，解得．

（2）①由（1）知，，则点的坐标为，

设在点处的切线交轴分别交于点，，

则的方程为，由此得．

故

②设，则，令，解得．

当时，，是减函数；

当时，是增函数．

从而，当时，函数有极小值，也是最小值，所以，

此时，

答：当时，公路的长度最短，最短长度为千米