Question

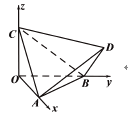
【题目】如图，已知四棱锥P－ABCD的底面是边长为1的正方形，且侧棱PC⊥底面ABCD，且PC＝2，E是侧棱PC上的动点

（1）求四棱锥P－ABCD的体积；

（2）证明：BD⊥AE。

（3）求二面角P-BD-C的正切值。

Answer 1

【答案】（1）（2）详见解析（3）

【解析】

试题分析：（1）四棱锥P-ABCD的体积V=S正方形ABCDPC，由此能求出结果．（2）连结AC，由已知条件条件出BD⊥AC，BD⊥PC，从而得到BD⊥平面PAC，不论点E在何位置，都有AE平面PAC，由此能证明BD⊥AE．

（3）以C为原点，CD为x轴，CB为y轴，CP为z轴，建立空间直角坐标系，利用向量法能求出二面角P-BD-C的正切值

试题解析：（1）该四棱锥P－ABCD的底面是边长为1的正方形，

侧棱PC⊥底面ABCD，且PC=2.

∴ …………4分

(2)连结AC，∵ABCD是正方形

∴BD⊥AC ∵PC⊥底面ABCD 且平面 ∴BD⊥PC …………6分

又∵∴BD⊥平面PAC

∵不论点E在何位置，都有AE平面PAC

∴BD⊥AE …………8分

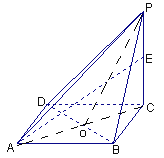
（3）设相交于，连,由四棱锥P－ABCD的底面是边长为1的正方形，PC⊥底面ABCD知，是二面角P-BD-C的的一个平面角， …………10分

,即二面角P-BD-C的正切值为.…………12分