题目内容
如图所示,已知点C的坐标是(2,2),过点C的直线CA与x轴交于点A,过点C且与直线CA垂直的

直线CB与y轴交于点B.设点M是线段AB的中点,求点M的轨迹方程.

直线CB与y轴交于点B.设点M是线段AB的中点,求点M的轨迹方程.
x+y-2=0
方法一(参数法):设M的坐标为(x,y).
若直线CA与x轴垂直,则可得到M的坐标为(1,1).
若直线CA不与x轴垂直,设直线CA的斜率为k,则直线CB的斜率为- ,故直线CA方程为:y=k(x-2)+2,
,故直线CA方程为:y=k(x-2)+2,
令y=0得x=2-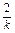 ,则A点坐标为
,则A点坐标为 .
.
CB的方程为:y=- (x-2)+2,令x=0,得y=2+
(x-2)+2,令x=0,得y=2+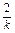 ,
,
则B点坐标为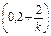 ,由中点坐标公式得M点的坐标为
,由中点坐标公式得M点的坐标为
 ①
①
消去参数k得到x+y-2="0" (x≠1),
点M(1,1)在直线x+y-2=0上,
综上所述,所求轨迹方程为x+y-2=0.
方法二 (直接法)设M(x,y),依题意A点坐标为(2x,0),B点坐标为(0,2y).
∵|MA|=|MC|,∴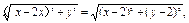 化简得x+y-2=0.
化简得x+y-2=0.
方法三 (定义法)依题意|MA|=|MC|=|MO|,
即:|MC|=|MO|,所以动点M是线段OC的中垂线,故由点斜式方程得到:x+y-2=0.
若直线CA与x轴垂直,则可得到M的坐标为(1,1).
若直线CA不与x轴垂直,设直线CA的斜率为k,则直线CB的斜率为-
 ,故直线CA方程为:y=k(x-2)+2,
,故直线CA方程为:y=k(x-2)+2,令y=0得x=2-
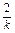 ,则A点坐标为
,则A点坐标为 .
.CB的方程为:y=-
 (x-2)+2,令x=0,得y=2+
(x-2)+2,令x=0,得y=2+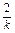 ,
,则B点坐标为
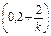 ,由中点坐标公式得M点的坐标为
,由中点坐标公式得M点的坐标为 ①
①消去参数k得到x+y-2="0" (x≠1),
点M(1,1)在直线x+y-2=0上,
综上所述,所求轨迹方程为x+y-2=0.
方法二 (直接法)设M(x,y),依题意A点坐标为(2x,0),B点坐标为(0,2y).
∵|MA|=|MC|,∴
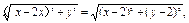 化简得x+y-2=0.
化简得x+y-2=0.方法三 (定义法)依题意|MA|=|MC|=|MO|,
即:|MC|=|MO|,所以动点M是线段OC的中垂线,故由点斜式方程得到:x+y-2=0.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 上的动点
上的动点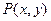 及两定点A(-2,0),B(2,0),直线PA,PB的斜率分别是
及两定点A(-2,0),B(2,0),直线PA,PB的斜率分别是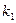 ,
,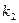 ,且
,且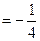 。(1)求动点P的轨迹C的方程;
。(1)求动点P的轨迹C的方程;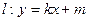 与曲线C交于M,N两点,且直线BM,BN的斜率都存在并满足
与曲线C交于M,N两点,且直线BM,BN的斜率都存在并满足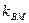 ·
·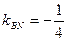 ,求证:直线
,求证:直线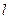 过原点。
过原点。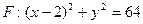 (F为圆心)上一点,线段AB的垂直平分线交BF于P.
(F为圆心)上一点,线段AB的垂直平分线交BF于P.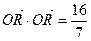 (O为原点),若存在,求直线l的方程,若不存在,请说明理由.
(O为原点),若存在,求直线l的方程,若不存在,请说明理由.

 的最值
的最值 平面上,
平面上,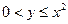 ,
,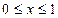 所围成图形的面积为
所围成图形的面积为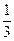 ,则集合
,则集合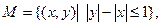
 的交集
的交集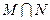 所表示的图形面积为
所表示的图形面积为  (C)
(C)  (B)
(B) 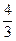 . ( )
. ( )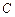 上的点的坐标
上的点的坐标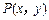 是方程
是方程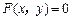 的解”是正确的,则下列命题一定正确的是( )
的解”是正确的,则下列命题一定正确的是( )
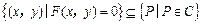
 ,焦点在
,焦点在 轴上,斜率为
轴上,斜率为 且过椭圆右焦点
且过椭圆右焦点 的直线交椭圆于
的直线交椭圆于 两点,
两点, 与
与 共线.设
共线.设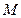 为椭圆上任意一点,且
为椭圆上任意一点,且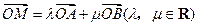 ,证明
,证明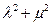 为定值.
为定值.