题目内容
知抛物线C:y2=4x,若椭圆左焦点及相应的准线与抛物线C的焦点F及准线l分别重合,试求椭圆短轴端点B与焦点F连线中点P的轨迹方程;
P点轨迹方程为y2=x-1(x>1)
【解题思路】探求动点满足的几何关系,在转化为方程
由抛物线y2=4x,得焦点F(1,0),准线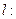 x=-1
x=-1
(1)设P(x,y),则B(2x-1,2y),
椭圆中心O′,则|FO′|∶|BF|=e,
又设点B到l的距离为d,则|BF|∶d=e,
∴|FO′|∶|BF|=|BF|∶d,即(2x-2)2+(2y)2=2x(2x-2),
化简得P点轨迹方程为y2=x-1(x>1)。
[名师指引] 求曲线方程的方法主要有:直接法、定义法、代入法、参数法,本题用到直接法,但题目条件需要转化
由抛物线y2=4x,得焦点F(1,0),准线
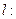 x=-1
x=-1(1)设P(x,y),则B(2x-1,2y),
椭圆中心O′,则|FO′|∶|BF|=e,
又设点B到l的距离为d,则|BF|∶d=e,
∴|FO′|∶|BF|=|BF|∶d,即(2x-2)2+(2y)2=2x(2x-2),
化简得P点轨迹方程为y2=x-1(x>1)。
[名师指引] 求曲线方程的方法主要有:直接法、定义法、代入法、参数法,本题用到直接法,但题目条件需要转化

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 的直线交(1)中轨迹P、Q两点,PQ的中垂线交
的直线交(1)中轨迹P、Q两点,PQ的中垂线交 轴N. 求三角形PQN的面积.
轴N. 求三角形PQN的面积.
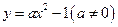 上有关于直线
上有关于直线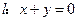 对称的不同的两点
对称的不同的两点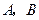 ,求实数
,求实数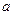 的取值范围.
的取值范围.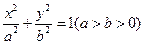 的左、右焦点分别是
的左、右焦点分别是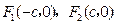 ,
,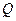 是椭圆外的动点,满足
是椭圆外的动点,满足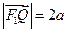 ,点
,点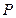 是线段
是线段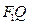 与该椭圆的交点,设
与该椭圆的交点,设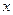 为点
为点 。
。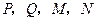 四点都在椭圆
四点都在椭圆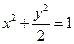 上,
上,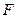 为椭圆在
为椭圆在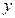 轴正半轴上的焦点.已知
轴正半轴上的焦点.已知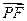 与
与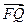 共线,
共线,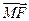 与
与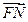 共线,且
共线,且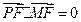 .求四边形
.求四边形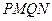 的面积的最小值和最大值.
的面积的最小值和最大值.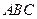 的顶点
的顶点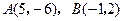 ,求
,求 的外接圆方程.
的外接圆方程.