题目内容
已知定点A(-2,0),动点B是圆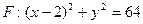 (F为圆心)上一点,线段AB的垂直平分线交BF于P.
(F为圆心)上一点,线段AB的垂直平分线交BF于P.
(1)求动点P的轨迹方程;
(2)是否存在过点E(0,-4)的直线l交P点的轨迹于点R,T,且满足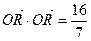 (O为原点),若存在,求直线l的方程,若不存在,请说明理由.
(O为原点),若存在,求直线l的方程,若不存在,请说明理由.
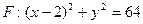 (F为圆心)上一点,线段AB的垂直平分线交BF于P.
(F为圆心)上一点,线段AB的垂直平分线交BF于P.(1)求动点P的轨迹方程;
(2)是否存在过点E(0,-4)的直线l交P点的轨迹于点R,T,且满足
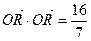 (O为原点),若存在,求直线l的方程,若不存在,请说明理由.
(O为原点),若存在,求直线l的方程,若不存在,请说明理由.(1) (2)
(2)
 (2)
(2)
(1)由题意:∵|PA|=|PB|且|PB|+|PF|=r=8
∴|PA|+|PF|=8>|AF|
∴P点轨迹为以A、F为焦点的椭圆…………………………3分
设方程为
 ………………………5分
………………………5分
(2)假设存在满足题意的直线l,其斜率存在,设为k,设


∴|PA|+|PF|=8>|AF|
∴P点轨迹为以A、F为焦点的椭圆…………………………3分
设方程为

 ………………………5分
………………………5分(2)假设存在满足题意的直线l,其斜率存在,设为k,设




练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 轴上,离心率为
轴上,离心率为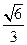 ,两条准线间的距离为6. 椭圆W的左焦点为
,两条准线间的距离为6. 椭圆W的左焦点为 ,过左准线与
,过左准线与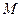 任作一条斜率不为零的直线
任作一条斜率不为零的直线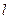 与椭圆W交于不同的两点
与椭圆W交于不同的两点 、
、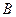 ,点
,点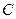 .
.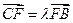 (
( );
); 面积
面积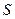 的最大值.
的最大值. 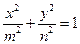 (
(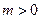 ,
,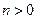 )的右焦点与抛物线
)的右焦点与抛物线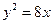 的焦点相同,离心率为
的焦点相同,离心率为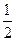 ,则此椭圆的方程为
,则此椭圆的方程为



 作直线与抛物线
作直线与抛物线 有且只有一个公共点,则这样的直线有( )
有且只有一个公共点,则这样的直线有( )
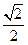 ,椭圆上的点到焦点的最短距离为1-
,椭圆上的点到焦点的最短距离为1-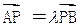 .
. 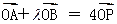 ,求m的取值范围.
,求m的取值范围.
 的直线交(1)中轨迹P、Q两点,PQ的中垂线交
的直线交(1)中轨迹P、Q两点,PQ的中垂线交 轴N. 求三角形PQN的面积.
轴N. 求三角形PQN的面积.
 中,
中, ,AC、BC边上的高分别为BD、AE,则以A、B为焦点,且过D、E的椭圆与双曲线的离心率的倒数和为 ( )
,AC、BC边上的高分别为BD、AE,则以A、B为焦点,且过D、E的椭圆与双曲线的离心率的倒数和为 ( ) B.
B. C.
C. D.
D.
