题目内容
已知椭圆的中心为坐标原点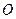 ,焦点在
,焦点在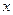 轴上,斜率为
轴上,斜率为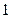 且过椭圆右焦点
且过椭圆右焦点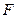 的直线交椭圆于
的直线交椭圆于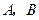 两点,
两点,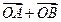 与
与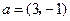 共线.设
共线.设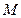 为椭圆上任意一点,且
为椭圆上任意一点,且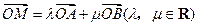 ,证明
,证明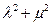 为定值.
为定值.
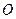 ,焦点在
,焦点在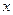 轴上,斜率为
轴上,斜率为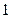 且过椭圆右焦点
且过椭圆右焦点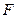 的直线交椭圆于
的直线交椭圆于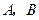 两点,
两点,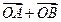 与
与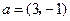 共线.设
共线.设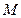 为椭圆上任意一点,且
为椭圆上任意一点,且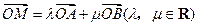 ,证明
,证明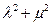 为定值.
为定值.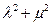 为定值,定值为
为定值,定值为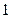
由题意可知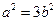 ,所以椭圆
,所以椭圆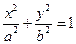 可化为
可化为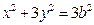 .
.
设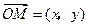 ,由已知得
,由已知得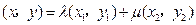 ,
,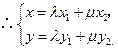
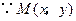 在椭圆上,
在椭圆上,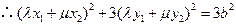 .
.
即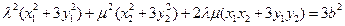 . ①
. ①
由(Ⅰ)知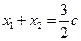 ,
,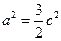 ,
,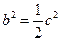 .
.
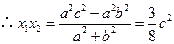 .
.
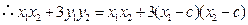
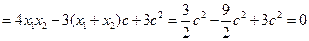 .
.
又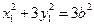 ,
,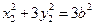 ,代入①得
,代入①得 .
.
故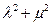 为定值,定值为
为定值,定值为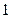 .
.
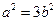 ,所以椭圆
,所以椭圆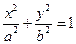 可化为
可化为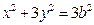 .
.设
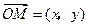 ,由已知得
,由已知得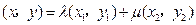 ,
,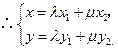
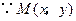 在椭圆上,
在椭圆上,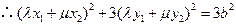 .
.即
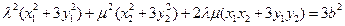 . ①
. ①由(Ⅰ)知
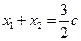 ,
,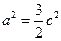 ,
,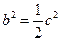 .
.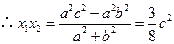 .
.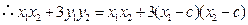
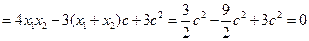 .
.又
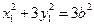 ,
,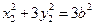 ,代入①得
,代入①得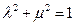 .
.故
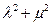 为定值,定值为
为定值,定值为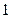 .
.
练习册系列答案
相关题目

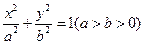 的左、右焦点分别是
的左、右焦点分别是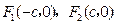 ,
,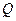 是椭圆外的动点,满足
是椭圆外的动点,满足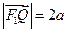 ,点
,点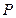 是线段
是线段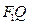 与该椭圆的交点,设
与该椭圆的交点,设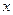 为点
为点 。
。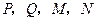 四点都在椭圆
四点都在椭圆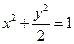 上,
上,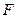 为椭圆在
为椭圆在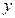 轴正半轴上的焦点.已知
轴正半轴上的焦点.已知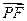 与
与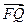 共线,
共线,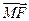 与
与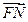 共线,且
共线,且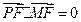 .求四边形
.求四边形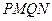 的面积的最小值和最大值.
的面积的最小值和最大值.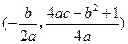 ,准线方程是
,准线方程是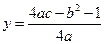 ,求证:抛物线的方程为
,求证:抛物线的方程为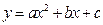 .
.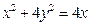 上,求使
上,求使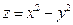 取得最大值和最小值的点
取得最大值和最小值的点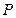 的坐标.
的坐标.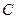 的中心在坐标原点,左顶点
的中心在坐标原点,左顶点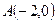 ,离心率
,离心率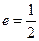 ,
,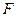 为右焦点,过焦点
为右焦点,过焦点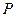 、
、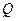 两点(不同于点
两点(不同于点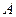 ).
).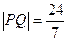 时,求直线PQ的方程;
时,求直线PQ的方程;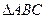 能否成为等边三角形,并说明理由.
能否成为等边三角形,并说明理由.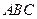 的顶点
的顶点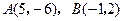 ,求
,求 的外接圆方程.
的外接圆方程.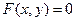 的点都在曲线
的点都在曲线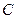 上,那么 ( )
上,那么 ( )