题目内容
7.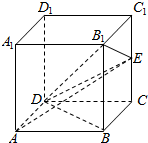 在棱长为4的正方体ABCD-A1B1C1D1中,设E是棱CC1的中点.
在棱长为4的正方体ABCD-A1B1C1D1中,设E是棱CC1的中点.(1)求证:BD⊥AE;
(2)求证:AC∥平面B1DE;
(3)求三棱锥A-B1DE的体积.
分析 (1)通过证明BD⊥平面AEC,得出BD⊥AE;
(2)通过△ACC1的中位线证明线线平行,再证明线面平行;
(3)点A到平面B1DE的距离等于点C到平面B1DE的距离,利用等积法求出三棱锥A-B1DE的体积.
解答 (1)证明:连接BD,AE,
∵四边形ABCD是正方形,∴BD⊥AC,
又∵EC⊥底面ABCD,BD?面ABCD,
∴EC⊥BD,且EC∩AC=C,
∴BD⊥平面AEC,
又AE?平面AEC,∴BD⊥AE;
(2)证明:连接AC1,设AC1∩B1D=G,
则G为AC1的中点,E为C1C的中点,
∴GE为△ACC1的中位线,
∴AC∥GE,GE?平面B1DE,AC?平面B1DE,
∴AC∥平面B1DE;
(3)解:由(2)知,点A到平面B1DE的距离等于点C到平面B1DE的距离,
∴三棱锥A-B1DE的体积是$\frac{1}{3}$×($\frac{1}{2}$×2×4)×4=$\frac{16}{3}$,
∴三棱锥A-B1DE的体积为$\frac{16}{3}$.
点评 本题考查了空间中的垂直与平行的判断与性质的应用问题,也考查了求几何体的体积的问题,是综合性题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.设z=ax+y中变量x、y满足条件$\left\{\begin{array}{l}{x-4y≤-3}\\{3x+5y≤25}\\{x≥1}\end{array}\right.$,若目标函数z仅在(5,2)处取得最大值,则a的取值范围是( )
| A. | (-∞,-$\frac{3}{5}$) | B. | ($\frac{1}{4}$,$\frac{3}{5}$) | C. | ($\frac{1}{4}$,+∞) | D. | ($\frac{3}{5}$,+∞) |
2.P点的直角坐标(-1,$\sqrt{3}$)化成极坐标为( )
| A. | (2,$\frac{2}{3}$π) | B. | ($\sqrt{2}$,$\frac{2}{3}$π) | C. | ($\sqrt{2}$,$\frac{4}{3}$π) | D. | (2,$\frac{4}{3}$π) |
19.已知,P(A)=0.3,P(B|A)=0.4,P(A|B)=0.2,则P(A+B)=( )
(其中P(A+B)=P(A)+P(B)-P(AB))
(其中P(A+B)=P(A)+P(B)-P(AB))
| A. | 0.90 | B. | 0.78 | C. | 0.60 | D. | 0.40 |
17.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2},x<0}\\{{2}^{x},x≥0}\end{array}\right.$,则f(f(-1))=( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{4}$ | D. | 2 |
 如图,AC⊥平面α,AB∥平面α,CD?平面α,M、N分别是AC、BD的中点,若AB=4,AC=2,CD=4,BD=6,
如图,AC⊥平面α,AB∥平面α,CD?平面α,M、N分别是AC、BD的中点,若AB=4,AC=2,CD=4,BD=6,