题目内容
19.已知,P(A)=0.3,P(B|A)=0.4,P(A|B)=0.2,则P(A+B)=( )(其中P(A+B)=P(A)+P(B)-P(AB))
| A. | 0.90 | B. | 0.78 | C. | 0.60 | D. | 0.40 |
分析 利用条件概率公式,求出P(AB),P(B),利用P(A+B)=P(A)+P(B)-P(AB),即可得出结论.
解答 解:∵P(A)=0.3,P(B|A)=0.4,
∴P(AB)=P(B|A)P(A)=0.12,
∵P(A|B)=0.2,
∴P(B)=0.6,
∴P(A+B)=P(A)+P(B)-P(AB)=0.3+0.6-0.12=0.78,
故选:B.
点评 本题考查条件概率,考查学生的计算能力,正确运用条件概率公式是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.若两点P(-1,3)、Q(2,b)的距离为$\sqrt{13}$,则b的值为( )
| A. | 2 | B. | 2或4 | C. | 1或5 | D. | 5 |
14.已知sin55°=m,则cos2015°=( )
| A. | $\sqrt{1-{m^2}}$ | B. | -$\sqrt{1-{m^2}}$ | C. | m | D. | -m |
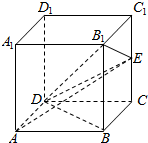 在棱长为4的正方体ABCD-A1B1C1D1中,设E是棱CC1的中点.
在棱长为4的正方体ABCD-A1B1C1D1中,设E是棱CC1的中点.