题目内容
2.P点的直角坐标(-1,$\sqrt{3}$)化成极坐标为( )| A. | (2,$\frac{2}{3}$π) | B. | ($\sqrt{2}$,$\frac{2}{3}$π) | C. | ($\sqrt{2}$,$\frac{4}{3}$π) | D. | (2,$\frac{4}{3}$π) |
分析 利用$\left\{\begin{array}{l}{ρ=\sqrt{{x}^{2}+{y}^{2}}}\\{tanθ=\frac{y}{x}}\end{array}\right.$即可得出.
解答 解:$ρ=\sqrt{(-1)^{2}+(\sqrt{3})^{2}}$=2,tanθ=-$\sqrt{3}$,θ∈$(\frac{π}{2},π)$,∴$θ=\frac{2π}{3}$.
∴点P的极坐标为$(2,\frac{2π}{3})$.
故选:A.
点评 本题考查了直角坐标化为极坐标的方法,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
10.若两点P(-1,3)、Q(2,b)的距离为$\sqrt{13}$,则b的值为( )
| A. | 2 | B. | 2或4 | C. | 1或5 | D. | 5 |
14.已知sin55°=m,则cos2015°=( )
| A. | $\sqrt{1-{m^2}}$ | B. | -$\sqrt{1-{m^2}}$ | C. | m | D. | -m |
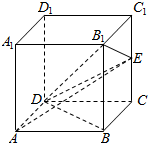 在棱长为4的正方体ABCD-A1B1C1D1中,设E是棱CC1的中点.
在棱长为4的正方体ABCD-A1B1C1D1中,设E是棱CC1的中点.