题目内容
12.已知圆M:x2+(y-2)2=1,Q是x轴上的动点,QA,QB分别切圆M于A,B两点.(1)若点Q的坐标为(-1,0),求切线QA,QB的方程;
(2)求四边形QAMB的面积的最小值.
分析 (1)分类讨论,利用圆心到直线的距离等于半径,即可求切线QA,QB的方程;
(2)连接QM,则易知四边形QAMB的面积$S=2{S_{△QAM}}=2×\frac{1}{2}×|{QA}||{MA}|=|{QA}|=\sqrt{{{|{QC}|}^2}-1}$,即可求四边形QAMB的面积的最小值.
解答 解:(1)由题意,过点(-1,0),且与x轴垂直的直线显然与圆M相切,此时,切线方程为x=-1
当过点(-1,0)的直线不与x轴垂直时,设其方程为y=k(x+1),即kx-y+k=0,
由$\frac{{|{-2+k}|}}{{\sqrt{{k^2}+1}}}=1$解得$k=\frac{3}{4}$,此时切线方程为3x-4y+3=0;
(2)连接QM,则易知四边形QAMB的面积S=2S△QAM=2×$\frac{1}{2}×|QA||MA|$=|QA|=$\sqrt{|QM{|}^{2}-1}$.
故当点Q为坐标原点时,${S_{min}}=\sqrt{3}$.
点评 本题考查直线与圆 的位置关系,考查面积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
2.通过随机询问110名性别不同的大学生是否爱好某项运动,其中有男生60名,调查发现,男、女生中分别有40人和20人爱好运动.
(Ⅰ)根据以上数据完成以下2×2列联表:
(Ⅱ)判断爱好该项运动与性别是否有关?
参考公式:K2=$\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$其中n=a+b+c+d
附表:
(Ⅰ)根据以上数据完成以下2×2列联表:
| 男 | 女 | 总计 | |
| 爱好 | |||
| 不爱好 | |||
| 总计 | 110 |
参考公式:K2=$\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$其中n=a+b+c+d
附表:
| p(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
2.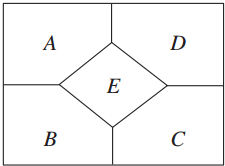 如图所示的五个区域中,现有四种颜色可供选择.要求每一个区域只涂一种颜色,相邻区域所涂颜色不同,则不同的涂色方法种数为( )
如图所示的五个区域中,现有四种颜色可供选择.要求每一个区域只涂一种颜色,相邻区域所涂颜色不同,则不同的涂色方法种数为( )
 如图所示的五个区域中,现有四种颜色可供选择.要求每一个区域只涂一种颜色,相邻区域所涂颜色不同,则不同的涂色方法种数为( )
如图所示的五个区域中,现有四种颜色可供选择.要求每一个区域只涂一种颜色,相邻区域所涂颜色不同,则不同的涂色方法种数为( )| A. | 24种 | B. | 48种 | C. | 72种 | D. | 96种 |
 如图,在△ABC和△AEF中,B是EF的中点,AB=EF=1,CA=CB=2,若$\overrightarrow{AB}$•$\overrightarrow{AE}$+
如图,在△ABC和△AEF中,B是EF的中点,AB=EF=1,CA=CB=2,若$\overrightarrow{AB}$•$\overrightarrow{AE}$+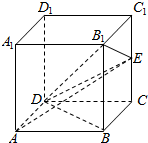 在棱长为4的正方体ABCD-A1B1C1D1中,设E是棱CC1的中点.
在棱长为4的正方体ABCD-A1B1C1D1中,设E是棱CC1的中点.