题目内容
16．已知a，b，c都是实数，求证：a2+b2+c2≥$\frac{（a+b+c）^{2}}{3}$．分析 利用（a+b+c）2=a2+b2+c2+2ab+2ac+2bc，再用基本不等式可证
解答 证明：∵（a+b+c）2=a2+b2+c2+2ab+2ac+2bc≤a2+b2+c2+a2+b2+a2+c2+b2+c2
∴3（a2+b2+c2）≥（a+b+c）2，
∴a2+b2+c2≥$\frac{（a+b+c）^{2}}{3}$．
点评 本题考查不等式的证明，考查基本不等式的运用，比较基础．
练习册系列答案
快捷英语周周练系列答案
相关题目
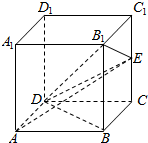在棱长为4的正方体ABCD-A1B1C1D1中，设E是棱CC1的中点．