题目内容
17.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2},x<0}\\{{2}^{x},x≥0}\end{array}\right.$,则f(f(-1))=( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{4}$ | D. | 2 |
分析 运用分段函数,可得f(-1)=1,再求f(f(-1))=f(1)=2.
解答 解:函数f(x)=$\left\{\begin{array}{l}{{x}^{2},x<0}\\{{2}^{x},x≥0}\end{array}\right.$,
则f(-1)=(-1)2=1,
f(f(-1))=f(1)=21=2.
故选D.
点评 本题考查分段函数和运用:求函数值,考查运算能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.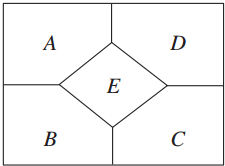 如图所示的五个区域中,现有四种颜色可供选择.要求每一个区域只涂一种颜色,相邻区域所涂颜色不同,则不同的涂色方法种数为( )
如图所示的五个区域中,现有四种颜色可供选择.要求每一个区域只涂一种颜色,相邻区域所涂颜色不同,则不同的涂色方法种数为( )
 如图所示的五个区域中,现有四种颜色可供选择.要求每一个区域只涂一种颜色,相邻区域所涂颜色不同,则不同的涂色方法种数为( )
如图所示的五个区域中,现有四种颜色可供选择.要求每一个区域只涂一种颜色,相邻区域所涂颜色不同,则不同的涂色方法种数为( )| A. | 24种 | B. | 48种 | C. | 72种 | D. | 96种 |
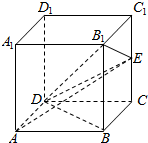 在棱长为4的正方体ABCD-A1B1C1D1中,设E是棱CC1的中点.
在棱长为4的正方体ABCD-A1B1C1D1中,设E是棱CC1的中点.