题目内容
18.设z=ax+y中变量x、y满足条件$\left\{\begin{array}{l}{x-4y≤-3}\\{3x+5y≤25}\\{x≥1}\end{array}\right.$,若目标函数z仅在(5,2)处取得最大值,则a的取值范围是( )| A. | (-∞,-$\frac{3}{5}$) | B. | ($\frac{1}{4}$,$\frac{3}{5}$) | C. | ($\frac{1}{4}$,+∞) | D. | ($\frac{3}{5}$,+∞) |
分析 作出不等式对应的平面区域,利用线性规划的知识,确定目标取最优解的条件,即可求出a的取值范围.
解答 解:作出不等式对应的平面区域,
由z=ax+y得y=-ax+z,
要使目标函数z=ax+y仅在点A(5,2)处取得最大值,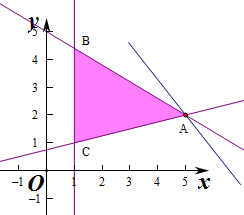
则阴影部分区域在直线y=-ax+z的下方,
∴-a<0,
即a>0,即目标函数的斜率k,满足k<kAB=-$\frac{3}{5}$,
即-a<-$\frac{3}{5}$,
则a>$\frac{3}{5}$,
即a的取值范围是($\frac{3}{5}$,+∞),
故选:D
点评 本题主要考查线性规划的应用,利用数形结合是解决线性规划题目的常用方法.根据条件目标函数z=ax+y仅在点(5,2)处取得最大值,确定直线的位置是解决本题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
10.若两点P(-1,3)、Q(2,b)的距离为$\sqrt{13}$,则b的值为( )
| A. | 2 | B. | 2或4 | C. | 1或5 | D. | 5 |
 如图,在△ABC和△AEF中,B是EF的中点,AB=EF=1,CA=CB=2,若$\overrightarrow{AB}$•$\overrightarrow{AE}$+
如图,在△ABC和△AEF中,B是EF的中点,AB=EF=1,CA=CB=2,若$\overrightarrow{AB}$•$\overrightarrow{AE}$+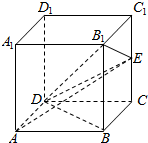 在棱长为4的正方体ABCD-A1B1C1D1中,设E是棱CC1的中点.
在棱长为4的正方体ABCD-A1B1C1D1中,设E是棱CC1的中点.