题目内容
17.数列{an}中,a1=2,${a_{n+1}}={a_n}+lg(1+\frac{1}{n})$,则a100=4.分析 由${a_{n+1}}={a_n}+lg(1+\frac{1}{n})$可得an+1-an=lg($\frac{n+1}{n}$),从而利用叠加法求和即可.
解答 解:∵${a_{n+1}}={a_n}+lg(1+\frac{1}{n})$,
∴an+1-an=lg($\frac{n+1}{n}$);
∴a2-a1=lg2,(1)
a3-a2=lg$\frac{3}{2}$,(2)
…
a100-a99=lg$\frac{100}{99}$,(99)
(1)+(2)+…+(99)得,
a100-a1=lg2+lg$\frac{3}{2}$+…+lg$\frac{100}{99}$=lg100=2,
故a100=a1+2=2+2=4;
故答案为:4.
点评 本题考查了数列的递推公式的化简与应用,同时考查了叠加法与对数的运算应用,属于中档题.

练习册系列答案
 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
2.通过随机询问110名性别不同的大学生是否爱好某项运动,其中有男生60名,调查发现,男、女生中分别有40人和20人爱好运动.
(Ⅰ)根据以上数据完成以下2×2列联表:
(Ⅱ)判断爱好该项运动与性别是否有关?
参考公式:K2=$\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$其中n=a+b+c+d
附表:
(Ⅰ)根据以上数据完成以下2×2列联表:
| 男 | 女 | 总计 | |
| 爱好 | |||
| 不爱好 | |||
| 总计 | 110 |
参考公式:K2=$\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$其中n=a+b+c+d
附表:
| p(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
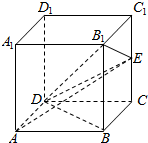 在棱长为4的正方体ABCD-A1B1C1D1中,设E是棱CC1的中点.
在棱长为4的正方体ABCD-A1B1C1D1中,设E是棱CC1的中点.