题目内容
某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:每一组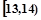 ;第二组
;第二组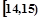 ,……,第五组
,……,第五组 .右图是按上述分组方法得到的频率分布直方图.
.右图是按上述分组方法得到的频率分布直方图. 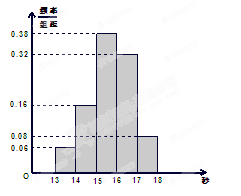
(I)若成绩大于或等于14秒且小于16秒认为良好,求该班在这次百米测试中成绩良好的人数;
(II)设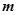 、
、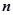 表示该班某两位同学的百米测试成绩,且已知
表示该班某两位同学的百米测试成绩,且已知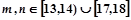 ,求事件“
,求事件“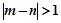 ”的概率.
”的概率.
(1)27;(2)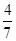
解析试题分析:(1)由直方图意义可得;(2)列举法一一列出总情况,利用古典概型公式解.
试题解析:(Ⅰ)由直方图知,成绩在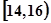 内的人数为:
内的人数为: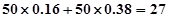 (人)
(人)
所以该班成绩良好的人数为27人.
(Ⅱ)由直方图知,成绩在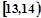 的人数为
的人数为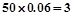 人,
人,
设为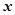 、
、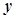 、
、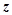 ;成绩在
;成绩在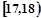 的人数为
的人数为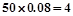 人,设为
人,设为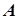 、
、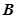 、
、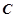 、
、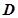 .
.
若 时,有
时,有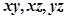 3种情况;
3种情况;
若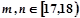 时,有
时,有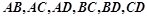 6种情况;
6种情况;
若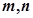 分别在
分别在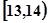 和
和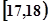 内时,
内时, A B C D x xA xB xC xD y yA yB yC yD z zA zB zC zD 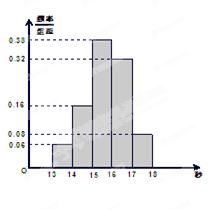
共有12种情况.
所以基本事件总数为21种. 记事件“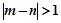 ”为事件E,则
”为事件E,则
事件E所包含的基本事件个数有12种.
∴P(E)=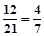 .
.
即事件“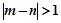 ”的概率为
”的概率为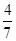 .
.
考点:直方图应用,古典概型.

某品牌汽车的4 店,对最近100位采用分期付款的购车者进行了统计,统计结果如下表所示:已知分3期付款的频率为0.2,且4
店,对最近100位采用分期付款的购车者进行了统计,统计结果如下表所示:已知分3期付款的频率为0.2,且4 店经销一辆该品牌的汽车,顾客若一次付款,其利润为1万元;若分2期付款或3期付款,其利润为1.5万元;若分4期付款或5期付款,其利润为2万元.用
店经销一辆该品牌的汽车,顾客若一次付款,其利润为1万元;若分2期付款或3期付款,其利润为1.5万元;若分4期付款或5期付款,其利润为2万元.用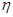 表示经销一辆该品牌汽车的利润.
表示经销一辆该品牌汽车的利润.
| 付款方式 | 一次 | 分2期 | 分3期 | 分4期 | 分5期 |
| 频数 | 40 | 20 | a | 10 | b |
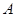 :“购买该品牌汽车的3位顾客中,至多有1位采用分3期付款”的概率
:“购买该品牌汽车的3位顾客中,至多有1位采用分3期付款”的概率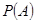 ;
;(2)求
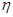 的分布列及其数学期望
的分布列及其数学期望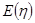 .
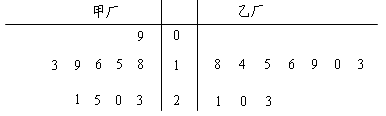
. 为了比较“传统式教学法”与我校所创立的“三步式教学法”的教学效果.共选100名学生随机分成两个班,每班50名学生,其中一班采取“传统式教学法”,二班实行“三步式教学法”
(Ⅰ)若全校共有学生2000名,其中男生1100名,现抽取100名学生对两种教学方式的受欢迎程度进行问卷调查,应抽取多少名女生?
(Ⅱ)下表1,2分别为实行“传统式教学”与“三步式教学”后的数学成绩:
表1
| 数学成绩 | 90分以下 | 90—120分 | 120—140分 | 140分以上 |
| 频 数 | 15 | 20 | 10 | 5 |
| 数学成绩 | 90分以下 | 90—120分 | 120—140分 | 140分以上 |
| 频 数 | 5 | 40 | 3 | 2 |
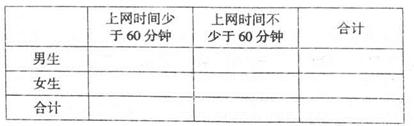
| 班 次 | 120分以下(人数) | 120分以上(人数) | 合计(人数) |
| 一班 | | | |
| 二班 | | | |
| 合计 | | | |
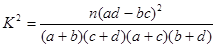 ,其中
,其中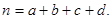
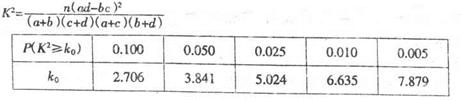
参考数据:
| P(K2≥k0) | 0.40 | 0.25 | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 0.708 | 1.323 | 2.706 | 3.841 | 6.635 | 7.879 |
某大学一个专业团队为某专业大学生研究了多款学习软件,其中有A、B、C三种软件投入使用,经一学年使用后,团队调查了这个专业大一四个班的使用情况,从各班抽取的样本人数如下表
| 班级 | 一 | 二 | 三 | 四 |
| 人数 | 3 | 2 | 3 | 4 |
(2)从这12名学生中,指定甲、乙、丙三人为代表,已知他们下午自习时间每人选择A、B两个软件学习的概率每个都是
 ,且他们选择A、B、C任一款软件都是相互独立的.设这三名学生中下午自习时间选软件C的人数为
,且他们选择A、B、C任一款软件都是相互独立的.设这三名学生中下午自习时间选软件C的人数为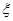 ,求
,求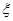 的分布列和数学期望.
的分布列和数学期望. 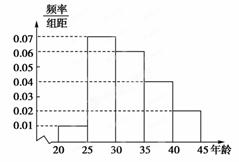
 的分布列及其数学期望
的分布列及其数学期望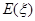 ;
;

 •
•
 的分布列和数学期望.
的分布列和数学期望.