题目内容
为了调査某大学学生在某天上网的时间,随机对lOO名男生和100名女生进行了不记名的问卷调查.得到了如下的统计结果:
表l:男生上网时间与频数分布表
表2:女生上网时间与频数分布表
(I)从这100名男生中任意选出3人,其中恰有1人上网时间少于60分钟的概率;
(II)完成下面的2X2列联表,并回答能否有90%的把握认为“大学生上网时间与性别有关”?
表3: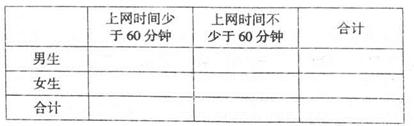 •
•
附: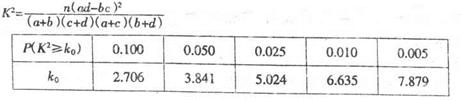
(Ⅰ)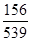 ;(Ⅱ)没有90%的把握认为“大学生上网时间与性别有关”.
;(Ⅱ)没有90%的把握认为“大学生上网时间与性别有关”.
解析试题分析:(Ⅰ)由男生上网时间频数分布表求出上网时间少于60分钟的人数和不少于60分钟的人数,任意选3人,恰有1人上网时间少于60分钟的选法有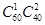 种,则易得概率恰有1人上网时间少于60分钟的
种,则易得概率恰有1人上网时间少于60分钟的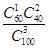 ;(Ⅱ)根据男生、女生的上网时间频数分布表易得2×2列联表,并由
;(Ⅱ)根据男生、女生的上网时间频数分布表易得2×2列联表,并由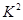 公式得出
公式得出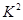 值,即得结论.
值,即得结论.
试题解析:(Ⅰ)由男生上网时间频数分布表可知100名男生中,上网时间少于60分钟的有60人,不少于60分钟的有40人, 2分
故从其中任选3人,恰有1人上网的时间少于60分钟的概率为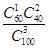 4分
4分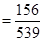 6分
6分
(Ⅱ)
8分 上网时间少于60分 上网时间不少于60分 合计 男生 60 40 100 女生 70 30 100 合计 130 70 200 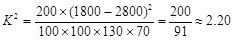 , 10分
, 10分
∵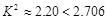 ,∴没有90%的把握认为“大学生上网时间与性别有关”. 12分
,∴没有90%的把握认为“大学生上网时间与性别有关”. 12分
考点:1、概率;2、独立性检验.

生产A,B两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品.现随机抽取这两种元件各100件进行检测,检测结果统计如下:
| 测试指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
| 元件A | 8 | 12 | 40 | 32 | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
(Ⅱ)生产一件元件A,若是正品可盈利40元,若是次品则亏损5元;生产一件元件B,若是正品可盈利50元,若是次品则亏损10元.在(Ⅰ)的前提下,
(ⅰ)记X为生产1件元件A和1件元件B所得的总利润,求随机变量X的分布列和数学期望;
(ⅱ)求生产5件元件B所获得的利润不少于140元的概率.
为了解甲、乙两厂的产品质量,采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取12件和5件,测量产品中微量元素x,y的含量(单位:毫克).下表是乙厂的5件产品的测量数据:
| 编号 | 1 | 2 | 3 | 4 | 5 |
| x | 169 | 178 | 166 | 175 | 180 |
| y | 75 | 80 | 77 | 76 | 81 |
(2)当产品中的微量元素x,y满足x≥175且y≥75,该产品为优等品,
①用上述样本数据估计乙厂生产的优等品的数量;
②从乙厂抽出的上述5件产品中,随机抽取2件,求抽取的2件产品中优等品数
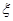 的分布列及其期望.
的分布列及其期望. 某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形的顶点)处都种了一株相同品种的作物。根据历年的种植经验,一株该种作物的年收货量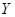 (单位:kg)与它的“相近”作物株数
(单位:kg)与它的“相近”作物株数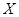 之间的关系如下表所示:
之间的关系如下表所示: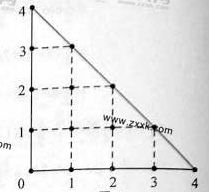
| X | 1 | 2 | 3 | 4 |
| Y | 51 | 48 | 45 | 42 |
这里,两株作物“相近”是指它们之间的直线距离不超过1米。
(Ⅰ)完成下表,并求所种作物的平均年收获量;
| Y | 51 | 48 | 45 | 42 |
| 频数 | | 4 | | |
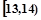 ;第二组
;第二组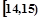 ,……,第五组
,……,第五组 .右图是按上述分组方法得到的频率分布直方图.
.右图是按上述分组方法得到的频率分布直方图. 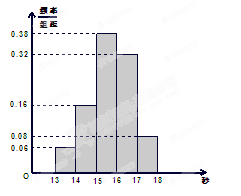
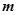 、
、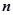 表示该班某两位同学的百米测试成绩,且已知
表示该班某两位同学的百米测试成绩,且已知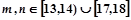 ,求事件“
,求事件“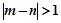 ”的概率.
”的概率.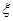 为四个小球得分总和.
为四个小球得分总和.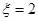 时的概率;
时的概率; 名同学参加某高校的自主招生面试,已知采用抽签的方式随机确定各考生的面试顺序(序号为
名同学参加某高校的自主招生面试,已知采用抽签的方式随机确定各考生的面试顺序(序号为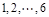 ).
).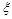 ,求随机变量
,求随机变量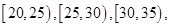
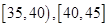 .
. 的值并根据频率分布直方图估计这500名志愿者中年龄在
的值并根据频率分布直方图估计这500名志愿者中年龄在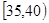 岁的人数;
岁的人数;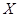 ,求
,求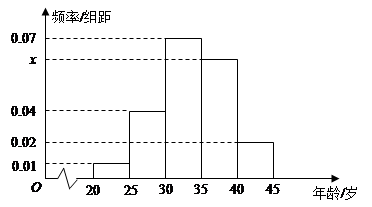
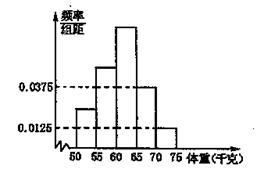
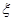 表示体重超过60千克的学生人数,求
表示体重超过60千克的学生人数,求