题目内容
某品牌汽车的4 店,对最近100位采用分期付款的购车者进行了统计,统计结果如下表所示:已知分3期付款的频率为0.2,且4
店,对最近100位采用分期付款的购车者进行了统计,统计结果如下表所示:已知分3期付款的频率为0.2,且4 店经销一辆该品牌的汽车,顾客若一次付款,其利润为1万元;若分2期付款或3期付款,其利润为1.5万元;若分4期付款或5期付款,其利润为2万元.用
店经销一辆该品牌的汽车,顾客若一次付款,其利润为1万元;若分2期付款或3期付款,其利润为1.5万元;若分4期付款或5期付款,其利润为2万元.用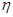 表示经销一辆该品牌汽车的利润.
表示经销一辆该品牌汽车的利润.
| 付款方式 | 一次 | 分2期 | 分3期 | 分4期 | 分5期 |
| 频数 | 40 | 20 | a | 10 | b |
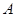 :“购买该品牌汽车的3位顾客中,至多有1位采用分3期付款”的概率
:“购买该品牌汽车的3位顾客中,至多有1位采用分3期付款”的概率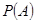 ;
;(2)求
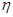 的分布列及其数学期望
的分布列及其数学期望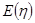 .
.
(1)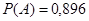 ;(2)
;(2)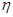 的分布列为:
的分布列为:
1 1.5 2 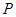
0.4 0.4 0.2 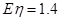 .
.
解析试题分析:(1)利用所有频数的和为100,频率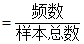 ,独立充富士见的概率求解;(2)经销一辆该品牌汽车的利润
,独立充富士见的概率求解;(2)经销一辆该品牌汽车的利润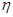 的取值分别为1,,1.5,2,列出分布列,用求数学期望的公式求解.
的取值分别为1,,1.5,2,列出分布列,用求数学期望的公式求解.
试题解析:(1)依题意,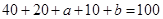 ,即
,即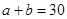 ,
,
又已知分3期付款的频率为0.2,则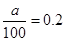 ,
,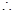
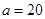 ,
,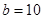 ,
,
若以频率作为概率,求事件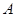 :“购买该品牌汽车的3位顾客中,至多有1位采用分3期付款”的概率
:“购买该品牌汽车的3位顾客中,至多有1位采用分3期付款”的概率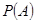 ;
;
则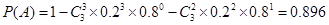 .
.
(2)依题意,经销一辆该品牌汽车的利润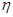 的取值分别为1,,1.5,2,
的取值分别为1,,1.5,2,
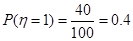 ,
,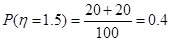 ,
,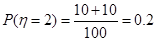 ,
,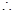
 的分布列为:
的分布列为: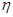
1 1.5 2 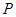
0.4 0.4 0.2 
 .
.
考点:古典概型,独立重复事件的概率,随机事件的分布列及期望.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,如下表所示.
| 一次购物量 | 1至4件 | 5至8件 | 9至12件 | 13至16件 | 17件及以上 |
| 顾客数(人) | x | 30 | 25 | y | 10 |
| 结算时间(分钟/人) | 1 | 1.5 | 2 | 2.5 | 3 |
(Ⅰ)确定x,y的值,并求顾客一次购物的结算时间X的分布列与数学期望;
(Ⅱ)若某顾客到达收银台时前面恰有2位顾客需结算,且各顾客的结算相互独立,求该顾客结算前的等候时间不超过2.5分钟的概率.
(注:将频率视为概率)
生产A,B两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品.现随机抽取这两种元件各100件进行检测,检测结果统计如下:
| 测试指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
| 元件A | 8 | 12 | 40 | 32 | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
(Ⅱ)生产一件元件A,若是正品可盈利40元,若是次品则亏损5元;生产一件元件B,若是正品可盈利50元,若是次品则亏损10元.在(Ⅰ)的前提下,
(ⅰ)记X为生产1件元件A和1件元件B所得的总利润,求随机变量X的分布列和数学期望;
(ⅱ)求生产5件元件B所获得的利润不少于140元的概率.
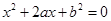 .
. 通晓日语,
通晓日语,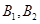 通晓俄语,
通晓俄语,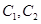 通晓韩语,从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
通晓韩语,从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.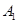 被选中的概率;(5分);(2)求
被选中的概率;(5分);(2)求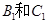 不全被选中的概率.(5分)
不全被选中的概率.(5分)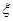 的分布列和数学期望.
的分布列和数学期望.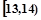 ;第二组
;第二组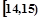 ,……,第五组
,……,第五组 .右图是按上述分组方法得到的频率分布直方图.
.右图是按上述分组方法得到的频率分布直方图. 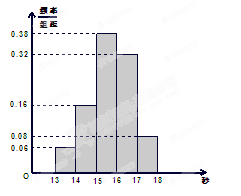
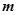 、
、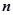 表示该班某两位同学的百米测试成绩,且已知
表示该班某两位同学的百米测试成绩,且已知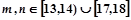 ,求事件“
,求事件“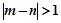 ”的概率.
”的概率.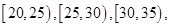
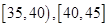 .
. 的值并根据频率分布直方图估计这500名志愿者中年龄在
的值并根据频率分布直方图估计这500名志愿者中年龄在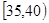 岁的人数;
岁的人数;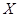 ,求
,求