题目内容
袋子里有完全相同的3只红球和4只黑球,今从袋子里随机取球.
(Ⅰ)若有放回地取3次,每次取一个球,求取出2个红球1个黑球的概率;
(Ⅱ)若无放回地取3次,每次取一个球,若取出每只红球得2分,取出每只黑球得1分,求得分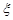 的分布列和数学期望.
的分布列和数学期望.
(1)108:343
(2)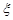
3 4 5 6 
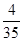
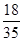
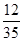
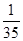
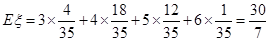
解析试题分析:解:(Ⅰ)从袋子里有放回地取3次球,相当于做了3次独立重复试验,每次试验取出红球的概率为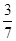 ,取出黑球的概率为
,取出黑球的概率为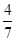 ,设事件
,设事件 “取出2个红球1个黑球”,则
“取出2个红球1个黑球”,则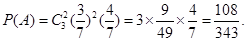 6分
6分
(Ⅱ)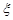 的取值有四个:3、4、5、6,分布列为:
的取值有四个:3、4、5、6,分布列为: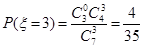 ,
,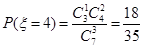 ,
,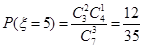 ,
,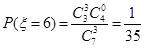 .
.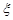
3 4 5 6 
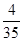
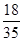
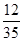
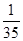
10分
从而得分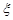 的数学期望
的数学期望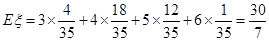 .0 12分
.0 12分
考点:分布列和期望
点评:主要是考查了分布列的求解以及期望值的运用,属于基础题。

练习册系列答案
相关题目
某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形的顶点)处都种了一株相同品种的作物。根据历年的种植经验,一株该种作物的年收货量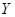 (单位:kg)与它的“相近”作物株数
(单位:kg)与它的“相近”作物株数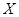 之间的关系如下表所示:
之间的关系如下表所示: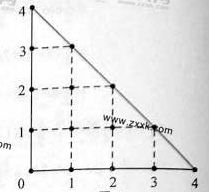
| X | 1 | 2 | 3 | 4 |
| Y | 51 | 48 | 45 | 42 |
这里,两株作物“相近”是指它们之间的直线距离不超过1米。
(Ⅰ)完成下表,并求所种作物的平均年收获量;
| Y | 51 | 48 | 45 | 42 |
| 频数 | | 4 | | |
某市直小学为了加强管理,对全校教职工实行新的临时事假制度:“每位教职工每月在正常的工作时间,临时有事,可请假至多三次,每次至多一小时”.现对该制度实施以来50名教职工请假的次数进行调查统计,结果如下表所示:
| 请假次数 |  | 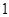 | 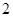 | 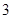 |
| 人数 | 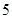 | 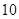 | 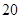 | 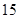 |
(1)从该小学任选两名教职工,用
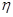 表示这两人请假次数之和,记“函数
表示这两人请假次数之和,记“函数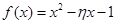 在区间
在区间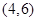 上有且只有一个零点”为事件
上有且只有一个零点”为事件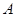 ,求事件
,求事件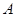 发生的概率
发生的概率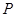 ;
;(2)从该小学任选两名职工,用
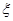 表示这两人请假次数之差的绝对值,求随机变量
表示这两人请假次数之差的绝对值,求随机变量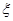 的分布列及数学期望
的分布列及数学期望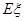 .
. 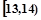 ;第二组
;第二组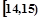 ,……,第五组
,……,第五组 .右图是按上述分组方法得到的频率分布直方图.
.右图是按上述分组方法得到的频率分布直方图. 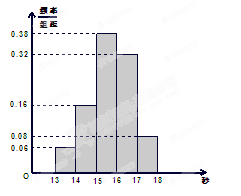
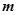 、
、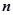 表示该班某两位同学的百米测试成绩,且已知
表示该班某两位同学的百米测试成绩,且已知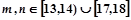 ,求事件“
,求事件“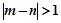 ”的概率.
”的概率.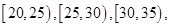
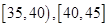 .
. 的值并根据频率分布直方图估计这500名志愿者中年龄在
的值并根据频率分布直方图估计这500名志愿者中年龄在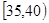 岁的人数;
岁的人数;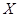 ,求
,求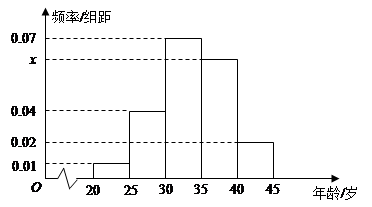
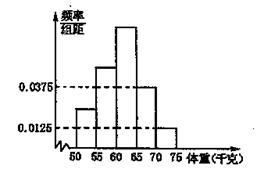
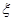 表示体重超过60千克的学生人数,求
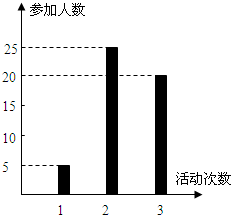
表示体重超过60千克的学生人数,求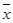 ;(II)从该班中任意选两名学生,求他们参加活动次数恰好相等的概率
;(II)从该班中任意选两名学生,求他们参加活动次数恰好相等的概率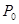 .
.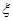 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量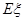 .
.
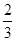 ,且每次射击的结果互不影响
,且每次射击的结果互不影响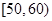 ,
, ,
,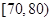 ,
,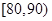 ,
,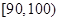 分别加以统计,得到如图所示的频率分布直方图.
分别加以统计,得到如图所示的频率分布直方图.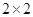 的列联表,并判断是否有
的列联表,并判断是否有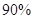 的把握认为“生产能手与工人所在的年龄组有关”?
的把握认为“生产能手与工人所在的年龄组有关”?