题目内容
1.已知两点M(-1,0)和N(1,0),若直线上存在点P,使|PM|+|PN|=4,则称该直线为“T型直线”.给出下列直线:①y=x+2;②y=-$\sqrt{3}$x+1;③y=-x-3;④y=$\frac{1}{2}$x+1,其中为“T型直线”的是( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
分析 根据椭圆的定义可得点P在以M,N 为焦点、长轴等于4的椭圆上,将问题转化为考查哪些直线和椭圆有交点,从而得到结论.
解答 解:满足|PM|+|PN|=4的点,在以M,N 为焦点、长轴等于4的椭圆上,椭圆的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.
①联立$\left\{\begin{array}{l}{y=x+2}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,得7x2-16x+4=0,
△=(-16)2-16×7>0,直线y=x+2和椭圆有两个交点,满足条件;
②联立$\left\{\begin{array}{l}{y=-\sqrt{3}x+1}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,得$15{x}^{2}-8\sqrt{3}x-16=0$,
△=$(-8\sqrt{3})^{2}+4×15×16>0$,直线y=-$\sqrt{3}$x+1和椭圆有两个交点,满足条件;
③联立$\left\{\begin{array}{l}{y=-x-3}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,得7x2+24x+24=0,
△=(24)2-4×7×24<0,直线y=-x-3与椭圆无交点,故不满足条件;
④联立$\left\{\begin{array}{l}{y=\frac{1}{2}x+1}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,得x2+x-4=0,
△=17>0,直线y=$\frac{1}{2}$x+1与椭圆有2个交点,故满足条件.
∴“T型直线”是①②④.
故选:B.
点评 本题考查椭圆的定义、直线和椭圆的位置关系,体现了数学转化思想方法,问题转化为考查直线和椭圆有无交点问题,是中档题.

| A. | 1与-2 | B. | 2与-2 | C. | 1与-1 | D. | 2与-1 |
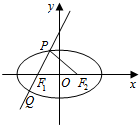 已知椭圆E的左、右焦点分别为F1、F2,过F1且斜率为2的直线交椭圆E于P、Q两点,若△PF1F2为直角三角形,则椭圆E的离心率为( )
已知椭圆E的左、右焦点分别为F1、F2,过F1且斜率为2的直线交椭圆E于P、Q两点,若△PF1F2为直角三角形,则椭圆E的离心率为( )| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{1}{3}$ |
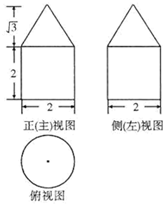
| A. | 6π | B. | 7π | C. | 8π | D. | 9π |