题目内容
9．
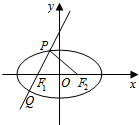已知椭圆E的左、右焦点分别为F1、F2，过F1且斜率为2的直线交椭圆E于P、Q两点，若△PF1F2为直角三角形，则椭圆E的离心率为（ ）| A． | $\frac{\sqrt{5}}{3}$ | B． | $\frac{2}{3}$ | C． | $\frac{\sqrt{2}}{3}$ | D． | $\frac{1}{3}$ |
分析 通过椭圆的定义可得PF1、PF2，利用勾股定理及离心率公式计算即得结论．
解答 解：由题可知：2=$\frac{P{F}_{2}}{P{F}_{1}}$，即PF2=2PF1，
又PF2+PF1=2a，∴PF1=$\frac{2}{3}a$，PF2=$\frac{4}{3}a$，
由勾股定理可知：$（2c）^{2}=（\frac{2}{3}a）^{2}+（\frac{4}{3}a）^{2}$，
即：${c}^{2}=\frac{5}{9}{a}^{2}$，
∴e=$\frac{c}{a}$=$\sqrt{\frac{{c}^{2}}{{a}^{2}}}$=$\sqrt{\frac{5}{9}}$=$\frac{\sqrt{5}}{3}$，
故选：A．
点评 本题考查求椭圆的离心率，涉及到三角函数的定义、勾股定理等基础知识，注意解题方法的积累，属于中档题．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
11．已知偶函数f（x）在区间（0，+∞）单调增加，则满足f（x-1）＜f（$\frac{1}{3}$）的x取值范围是（ ）
| A． | （-$\frac{1}{3}$，$\frac{1}{3}$） | B． | [-$\frac{1}{3}$，$\frac{1}{3}$] | C． | （$\frac{2}{3}$，$\frac{4}{3}$） | D． | [$\frac{2}{3}$，$\frac{4}{3}$] |
17．
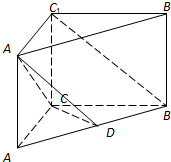如图所示，直三棱柱ABC-A1B1C1中，D是线段AB的中点，CA=CB=CC1=1，∠ACB=90°．
（1）证明：BC1∥面A1CD；
（2）求面A1CD与面A1C1CA所成的锐二面角的余弦值．
如图所示，直三棱柱ABC-A1B1C1中，D是线段AB的中点，CA=CB=CC1=1，∠ACB=90°．（1）证明：BC1∥面A1CD；
（2）求面A1CD与面A1C1CA所成的锐二面角的余弦值．
已知F1，F2是椭圆$\frac{x^2}{2}+\frac{y^2}{4}$=1的两焦点，P是椭圆在第一象限弧上一点，且满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$=1，若直线l：y=$\sqrt{2}$x+m（m∈（0，a]且a∈R）与椭圆交于A，B两点，