题目内容
6.已知抛物线C:y2=2px(p>0)的焦点为F,点F是双曲线:$\frac{3{x}^{2}}{5}$-$\frac{3{y}^{2}}{7}$=1的一个焦点;(1)求抛物线C的方程;
(2)过点F任作直线l与曲线C交于A,B两点.
①求$\overrightarrow{OA}$•$\overrightarrow{OB}$的值;②由点A,B分别向(x-2)2+y2=1各引一条切线切点分别为P、Q,记α=∠AFP,β=∠BFQ,求cosα+cosβ的值.
分析 (1)由已知条件推导出双曲线的焦点F1(-2,0),F2 (2,0),抛物线C焦点坐标F( $\frac{p}{2}$,0),从而得到 $\frac{p}{2}$=2,由此能求出抛物线的C的方程.
(2)①根据抛物线方程可得焦点F的坐标,设出直线的方程与抛物线方程联立消去x,设A,B的坐标分别为(x1,y1)(x2,y2)根据韦达定理可求得y1y2进而求得x1x2的值进而可得答案.
②对直线l的斜率分存在和不存在两种情况:把直线的方程与抛物线的方程联立,利用根与系数的关系及抛物线的定义即可得出.
解答 解:(1)双曲线C′:$\frac{3{x}^{2}}{5}$-$\frac{3{y}^{2}}{7}$=1中,
∵a2=$\frac{5}{3}$,b2=$\frac{7}{3}$,∴c=2,
∴双曲线的焦点F1(-2,0),F2 (2,0),
∵抛物线C:y2=2px(p>0)与双曲线C′:$\frac{3{x}^{2}}{5}$-$\frac{3{y}^{2}}{7}$=1的一个焦点相同,
且抛物线C:y2=2px(p>0)的焦点坐标F($\frac{p}{2}$,0),
∴$\frac{p}{2}$=2,解得p=4,
∴抛物线的C的方程是y2=8x.
(2)①根据抛物线方程y2=8x可得F(2,0)
设直线l的方程为x=my+2,将其与C的方程联立,消去x得y2-8my-16=0
设A,B的坐标分别为(x1,y1)(x2,y2)
则y1y2=-16
因为${y}_{1}^{2}$=8x1,${y}_{2}^{2}$=8x2,所以x1x2=4,
$\overrightarrow{OA}$•$\overrightarrow{OB}$=x1x2+y1y2=-12.
②当l不与x轴垂直时,设直线l的方程为y=k(x-2),
代入抛物线方程得k2x2-(4k2+8)x+4k2=0,
设A(x1,y1),B(x2,y2),则x1+x2=2k2+4,x1x2=4
∵cosα+cosβ=$\frac{\left|FP\right|}{\left|AF\right|}$+$\frac{\left|FQ\right|}{\left|BF\right|}$=$\frac{1}{{x}_{1}+2}+\frac{1}{{x}_{2}+2}$=$\frac{{x}_{1}+{x}_{2}+4}{{(x}_{1}+2)({x}_{2}+2)}$=$\frac{2{k}^{2}+8}{2(2{k}^{2}+8)}$=$\frac{1}{2}$,
当l与x轴垂直时,cosα+cosβ=$\frac{1}{2}$,
综上,cosα+cosβ=$\frac{1}{2}$.
点评 熟练掌握点到直线的距离公式、圆的标准方程及切线的性质、分类讨论的思想方法、直线的方程与抛物线的方程联立并利用根与系数的关系及抛物线的定义是解题的关键.

 阅读快车系列答案
阅读快车系列答案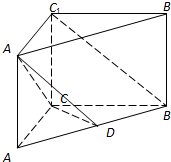 如图所示,直三棱柱ABC-A1B1C1中,D是线段AB的中点,CA=CB=CC1=1,∠ACB=90°.
如图所示,直三棱柱ABC-A1B1C1中,D是线段AB的中点,CA=CB=CC1=1,∠ACB=90°.(1)证明:BC1∥面A1CD;
(2)求面A1CD与面A1C1CA所成的锐二面角的余弦值.
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
| A. | y=$\frac{1}{x}$ | B. | y=x2+1 | C. | y=2x | D. | y=log2x |
| 月份x | 1 | 2 | 3 | 4 |
| 用水量y | 4.5 | 4 | 3 | 2.5 |
| A. | 5.15 | B. | 5.20 | C. | 5.25 | D. | 5.30 |
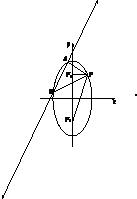 已知F1,F2是椭圆$\frac{x^2}{2}+\frac{y^2}{4}$=1的两焦点,P是椭圆在第一象限弧上一点,且满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$=1,若直线l:y=$\sqrt{2}$x+m(m∈(0,a]且a∈R)与椭圆交于A,B两点,
已知F1,F2是椭圆$\frac{x^2}{2}+\frac{y^2}{4}$=1的两焦点,P是椭圆在第一象限弧上一点,且满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$=1,若直线l:y=$\sqrt{2}$x+m(m∈(0,a]且a∈R)与椭圆交于A,B两点,