题目内容

13．已知N（2，0），M是y2=8x上的动点，则|MN|的最小值是2．

分析 设M（x，y），则|MN|=$\sqrt{（x-2）^{2}+{y}^{2}}$=x+2，结合x≥0，可得|MN|的最小值．

解答 解：设M（x，y），则|MN|=$\sqrt{（x-2）^{2}+{y}^{2}}$=x+2，
∵x≥0，
∴x+2≥2，
∴|MN|的最小值是2．
故答案为：2．

点评 本题考查抛物线的方程与性质，考查学生的计算能力，比较基础．

练习册系列答案
相关题目
15．关于x的方程ax=x${\;}^{\frac{1}{lo{g}_{3}x}}$有小于3的实数根，求a的取值范围．
4．下列说法正确的是①②③④．
①函数y=kx+b（k≠0，x∈R）有且只有一个零点；
②单调函数在其定义域内的零点至多有一个；
③指数函数在其定义域内没有零点；
④对数函数在其定义域内只有一个零点；
⑤幂函数在其定义域内至少有一个零点．
1．已知两点M（-1，0）和N（1，0），若直线上存在点P，使|PM|+|PN|=4，则称该直线为“T型直线”．给出下列直线：①y=x+2；②y=-$\sqrt{3}$x+1；③y=-x-3；④y=$\frac{1}{2}$x+1，其中为“T型直线”的是（　　）
A．①②③B．①②④C．①③④D．②③④
8．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{3}}{2}$，过其左焦点且与其长轴垂直的椭圆C的弦长为1．
（1）求椭圆C的方程
（2）求与椭圆C交于两点且过点（0，$\sqrt{3}$）的直线l的斜率k的取值范围．
18．已知公差不为0的等差数列{an}的首项a1=2，$\frac{1}{{a}_{1}}$，$\frac{1}{{a}_{2}}$，$\frac{1}{{a}_{4}}$成等比数列．
（1）求数列{an}的通项公式；
（2）若数列{bn}满足b1=1，an=log2（bn+1-bn），求数列{bn}的前n项和Sn．
5．已知函数f（x）=$\left\{\begin{array}{l}{0，x=0}\\{\frac{lnx}{x}，x＞0}\end{array}\right.$，g（x）=|sin$\frac{π}{2}$x|，则f（x）与g（x）的图象在区间[0，6]上的交点个数为（　　）
A．5B．6C．7D．8
2．如图所示，程序框图（算法流程图）的输出结果为（　　）
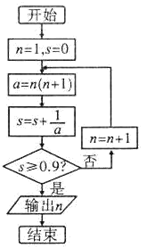
A．7B．8C．9D．10
3．如图所示的茎叶图记录了甲、乙两组各5名学生在一次英语口语测试中的成绩（单位：分），已知甲组数据的平均数为17，乙组数据的中位数为17，则甲、乙两组数据的方差较小的是（　　）
A．甲B．乙C．甲、乙相等D．无法确定

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网