题目内容
12.设F1、F2分别是椭圆$\frac{x^2}{4}$+y2=1的左、右焦点,若Q是该椭圆上的一个动点,则$\overrightarrow{Q{F_1}}$•$\overrightarrow{Q{F_2}}$的最大值和最小值分别为( )| A. | 1与-2 | B. | 2与-2 | C. | 1与-1 | D. | 2与-1 |
分析 椭圆$\frac{x^2}{4}$+y2=1中,a=2,b=1,c=$\sqrt{3}$,设Q(x,y),则$\overrightarrow{Q{F_1}}$•$\overrightarrow{Q{F_2}}$=(-$\sqrt{3}$-x,-y)•($\sqrt{3}$-x,-y)=x2+y2-3,由x∈[-2,2],能求出$\overrightarrow{Q{F_1}}$•$\overrightarrow{Q{F_2}}$的最大值和最小值.
解答 解:椭圆$\frac{x^2}{4}$+y2=1中,a=2,b=1,c=$\sqrt{3}$,
∴F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0),
设Q(x,y),则$\overrightarrow{Q{F_1}}$•$\overrightarrow{Q{F_2}}$=(-$\sqrt{3}$-x,-y)•($\sqrt{3}$-x,-y)=x2+y2-3,
∵x∈[-2,2],∴当x=0,即点Q为椭圆短轴端点时,$\overrightarrow{Q{F_1}}$•$\overrightarrow{Q{F_2}}$有最小值-2.
当x=±2,即点Q为椭圆长轴端点时,$\overrightarrow{Q{F_1}}$•$\overrightarrow{Q{F_2}}$有最大值1.
故选:A.
点评 本题考查直线与椭圆的位置关系的综合运用,具体涉及到椭圆的简单性质、向量的数量积公式等基本知识点,解题时要认真审题,仔细解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.函数$f(x)=sin(\frac{1}{3}x-\frac{π}{3})$的一个单调增区间为( )
| A. | $[-\frac{3}{2}π,π]$ | B. | $[\frac{5}{2}π,3π]$ | C. | $[-\frac{5}{6}π,-\frac{π}{2}]$ | D. | $[-\frac{1}{2}π,\frac{5π}{2}]$ |
7. 如图,在正方体中ABCD-A1B1C1D1,M为BC的中点,点N在四边形CDD1C1及其内部运动.若MN⊥A1C1,则N点的轨迹为( )
如图,在正方体中ABCD-A1B1C1D1,M为BC的中点,点N在四边形CDD1C1及其内部运动.若MN⊥A1C1,则N点的轨迹为( )
 如图,在正方体中ABCD-A1B1C1D1,M为BC的中点,点N在四边形CDD1C1及其内部运动.若MN⊥A1C1,则N点的轨迹为( )
如图,在正方体中ABCD-A1B1C1D1,M为BC的中点,点N在四边形CDD1C1及其内部运动.若MN⊥A1C1,则N点的轨迹为( )| A. | 线段 | B. | 圆的一部分 | C. | 椭圆的一部分 | D. | 双曲线的一部分 |
17.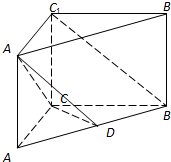 如图所示,直三棱柱ABC-A1B1C1中,D是线段AB的中点,CA=CB=CC1=1,∠ACB=90°.
如图所示,直三棱柱ABC-A1B1C1中,D是线段AB的中点,CA=CB=CC1=1,∠ACB=90°.
(1)证明:BC1∥面A1CD;
(2)求面A1CD与面A1C1CA所成的锐二面角的余弦值.
 如图所示,直三棱柱ABC-A1B1C1中,D是线段AB的中点,CA=CB=CC1=1,∠ACB=90°.
如图所示,直三棱柱ABC-A1B1C1中,D是线段AB的中点,CA=CB=CC1=1,∠ACB=90°.(1)证明:BC1∥面A1CD;
(2)求面A1CD与面A1C1CA所成的锐二面角的余弦值.
1.已知两点M(-1,0)和N(1,0),若直线上存在点P,使|PM|+|PN|=4,则称该直线为“T型直线”.给出下列直线:①y=x+2;②y=-$\sqrt{3}$x+1;③y=-x-3;④y=$\frac{1}{2}$x+1,其中为“T型直线”的是( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
2.如图所示,程序框图(算法流程图)的输出结果为( )
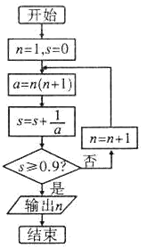

| A. | 7 | B. | 8 | C. | 9 | D. | 10 |