题目内容
16.已知棱长为a的正四面体可以在一个单位正方体(棱长为1)内任意地转动.设P,Q分别是正四面体与正方体的任意一顶点,当a达到最大值时,P,Q两点间距离的最小值是$\frac{\sqrt{3}-1}{2}$.分析 由题意判断出正四面体是单位正方体的内接球的内接正四面体,画出图象再求出最小距离值.
解答 解:由题意可知,正四面体只需在单位正方体的内接球内,
即是正四面体是单位正方体的内接球的内接正四面体,如图:
先作正方体的内切球O,点H是右侧面的中心,在球O上,P为正方体的顶点,
内切球与体对角线交于点Q,此时PQ间的距离取得最小值,
因为正方体的棱长为1,则内接球的半径为$\frac{1}{2}$,
所以|PQ|=$\frac{\sqrt{3}}{2}-\frac{1}{2}$=$\frac{\sqrt{3}-1}{2}$,
故答案为:$\frac{\sqrt{3}-1}{2}$.
点评 本题考查了正方体、内接球和内接四面体的关系,考查了空间想象能力,属于中档题.

练习册系列答案
相关题目
7.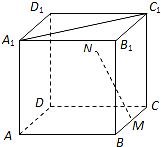 如图,在正方体中ABCD-A1B1C1D1,M为BC的中点,点N在四边形CDD1C1及其内部运动.若MN⊥A1C1,则N点的轨迹为( )
如图,在正方体中ABCD-A1B1C1D1,M为BC的中点,点N在四边形CDD1C1及其内部运动.若MN⊥A1C1,则N点的轨迹为( )
 如图,在正方体中ABCD-A1B1C1D1,M为BC的中点,点N在四边形CDD1C1及其内部运动.若MN⊥A1C1,则N点的轨迹为( )
如图,在正方体中ABCD-A1B1C1D1,M为BC的中点,点N在四边形CDD1C1及其内部运动.若MN⊥A1C1,则N点的轨迹为( )| A. | 线段 | B. | 圆的一部分 | C. | 椭圆的一部分 | D. | 双曲线的一部分 |
1.已知两点M(-1,0)和N(1,0),若直线上存在点P,使|PM|+|PN|=4,则称该直线为“T型直线”.给出下列直线:①y=x+2;②y=-$\sqrt{3}$x+1;③y=-x-3;④y=$\frac{1}{2}$x+1,其中为“T型直线”的是( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
6.已知抛物线y2=4x上两个动点B、C和点A(1,2),且∠BAC=90°,则动直线BC必过定点( )
| A. | (2,5) | B. | (-2,5) | C. | (5,-2) | D. | (5,2) |