题目内容
11.以直角坐标系的原点为极点,x轴正半轴为极轴,并在两种坐标系中取相同的长度单位,已知直线l的极坐标方程为ρsin(θ-$\frac{π}{3}$)=6,圆C的参数方程为$\left\{\begin{array}{l}{x=10cosθ}\\{y=10sinθ}\end{array}\right.$,(θ为参数).(1)求直线l的直角坐标方成;
(2)求直线l被圆截得得弦长.
分析 (1)直线l的极坐标方程为ρsin(θ-$\frac{π}{3}$)=6,展开并且把$\left\{\begin{array}{l}{x=ρcosθ}\\{y=ρsinθ}\end{array}\right.$代入即可得出;
(2)利用cos2θ+sin2θ=1即可把圆C的参数方程为$\left\{\begin{array}{l}{x=10cosθ}\\{y=10sinθ}\end{array}\right.$,(θ为参数),化为普通方程,利用点到直线的距离公式可得:圆心(0,0)到直线l的距离d,即可得出直线l被圆截得得弦长=2$\sqrt{{r}^{2}-{d}^{2}}$.
解答 解:(1)直线l的极坐标方程为ρsin(θ-$\frac{π}{3}$)=6,展开为$\frac{1}{2}ρsinθ-\frac{\sqrt{3}}{2}$ρcosθ=6,化为$\sqrt{3}$x-y+12=0.
(2)圆C的参数方程为$\left\{\begin{array}{l}{x=10cosθ}\\{y=10sinθ}\end{array}\right.$,(θ为参数),化为x2+y2=100,
圆心(0,0)到直线l的距离d=$\frac{12}{\sqrt{(\sqrt{3})^{2}+1}}$=6,
∴直线l被圆截得得弦长=2$\sqrt{1{0}^{2}-{6}^{2}}$=16.
点评 本题考查了极坐标方程化为直角坐标方程、参数方程化为普通方程、点到直线的距离公式、弦长公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
1.已知两点M(-1,0)和N(1,0),若直线上存在点P,使|PM|+|PN|=4,则称该直线为“T型直线”.给出下列直线:①y=x+2;②y=-$\sqrt{3}$x+1;③y=-x-3;④y=$\frac{1}{2}$x+1,其中为“T型直线”的是( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
2.如图所示,程序框图(算法流程图)的输出结果为( )
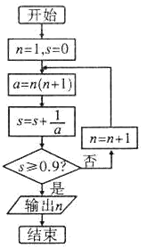

| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
6.已知抛物线y2=4x上两个动点B、C和点A(1,2),且∠BAC=90°,则动直线BC必过定点( )
| A. | (2,5) | B. | (-2,5) | C. | (5,-2) | D. | (5,2) |
16.如表是某厂1-4月份用水量(单位:百吨)的一组数据:由散点图可知,用水量y与月份x之间有线性相关关系,其线性回归方程是$\widehat{y}$=-0.7x+$\widehat{a}$,则$\widehat{a}$=( )
| 月份x | 1 | 2 | 3 | 4 |
| 用水量y | 4.5 | 4 | 3 | 2.5 |
| A. | 5.15 | B. | 5.20 | C. | 5.25 | D. | 5.30 |
 如图所示的茎叶图记录了甲、乙两组各5名学生在一次英语口语测试中的成绩(单位:分),已知甲组数据的平均数为17,乙组数据的中位数为17,则甲、乙两组数据的方差较小的是( )
如图所示的茎叶图记录了甲、乙两组各5名学生在一次英语口语测试中的成绩(单位:分),已知甲组数据的平均数为17,乙组数据的中位数为17,则甲、乙两组数据的方差较小的是( )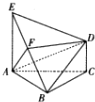 如图,在多面体ABCDE中,EA⊥平面ABC,DC∥EA且EA=2DC,CA=CB,F为BE的中点.
如图,在多面体ABCDE中,EA⊥平面ABC,DC∥EA且EA=2DC,CA=CB,F为BE的中点.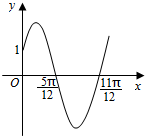 已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.