题目内容
9.设x、y∈R且满足$\left\{\begin{array}{l}{x≥1}\\{x-2y+3≥0}\\{y≥x}\end{array}\right.$,则z=x-2y的最大值等于-1.分析 先画出满足条件的平面区域,再将z=x-2y变形为:y=$\frac{1}{2}$x-$\frac{1}{2}$z,显然,直线过A(1,1)时,z最大,代入求出即可.
解答 解:画出满足条件的平面区域,如图示: ,
,
由z=x-2y得:y=$\frac{1}{2}$x-$\frac{1}{2}$z,
显然,直线过A(1,1)时,z最大,
∴z最大值=-1,
故答案为:-1.
点评 本题考察了简单的线性规划问题,考察数形结合思想,是一道基础题.

练习册系列答案
相关题目
14.下列各组中的两个函数是同一函数的是( )
| A. | f(x)=$\frac{{x}^{2}-1}{x-1}$和f(x)=x+1 | |
| B. | f(r)=πr2(r≥0)和g(x)=πx2(x≥0) | |
| C. | f(x)=logaax(a>0且a≠1)和g(x)=${a}^{lo{g}_{a}x}$(a>0且a≠1) | |
| D. | f(x)=x和g(t)和g(t)=$\sqrt{{t}^{2}}$ |
18.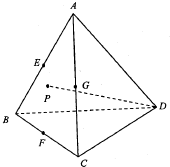 如图E、F、G分别是各棱长均相等的三棱锥A-BCD的棱AB、BC、AC的中点,点P在侧面ABC及其边界上运动,DP⊥AB,则动点P的轨迹是( )
如图E、F、G分别是各棱长均相等的三棱锥A-BCD的棱AB、BC、AC的中点,点P在侧面ABC及其边界上运动,DP⊥AB,则动点P的轨迹是( )
 如图E、F、G分别是各棱长均相等的三棱锥A-BCD的棱AB、BC、AC的中点,点P在侧面ABC及其边界上运动,DP⊥AB,则动点P的轨迹是( )
如图E、F、G分别是各棱长均相等的三棱锥A-BCD的棱AB、BC、AC的中点,点P在侧面ABC及其边界上运动,DP⊥AB,则动点P的轨迹是( )| A. | 线段FG | B. | 线段EG | C. | 线段EF | D. | 线段EC |
 在一段时间内有100辆汽车经过某交通岗,有2辆汽车速度小于35km/h,有3辆汽车的速度大于75km/h,时速(单位:km/h)频率分布直方图如图所示,
在一段时间内有100辆汽车经过某交通岗,有2辆汽车速度小于35km/h,有3辆汽车的速度大于75km/h,时速(单位:km/h)频率分布直方图如图所示,