题目内容
19.已知:P,Q是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上两点,O为椭圆中心,OP⊥OQ,求证:(1)$\frac{1}{|OP{|}^{2}}$+$\frac{1}{|OQ{|}^{2}}$=$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$;
(2)O到直线PQ的距离为定值.
分析 (1)通过设OP方程、OQ方程,分别与椭圆方程联立,利用两点间距离公式计算即得结论;
(2)通过O到直线PQ的距离d即为△POQ斜边上的高,计算即得结论.
解答 证明:(1)设OP方程为:y=kx(k≠0),
则OQ方程为:y=-$\frac{1}{k}$x,
联立$\left\{\begin{array}{l}{y=kx}\\{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$,可得:${{x}_{P}}^{2}$=$\frac{{a}^{2}+{b}^{2}}{{k}^{2}{a}^{2}+{b}^{2}}$,
∴|OP|2=(1+k2)•${{x}_{P}}^{2}$=$\frac{{a}^{2}{b}^{2}(1+{k}^{2})}{{a}^{2}{k}^{2}+{b}^{2}}$,
同理可得:|OQ|2=$\frac{{a}^{2}{b}^{2}(1+{k}^{-2})}{{k}^{-2}{a}^{2}+{b}^{2}}$=$\frac{{a}^{2}{b}^{2}(1+{k}^{2})}{{k}^{2}{b}^{2}+{a}^{2}}$,
于是$\frac{1}{|OP{|}^{2}}$+$\frac{1}{|OQ{|}^{2}}$=$\frac{{a}^{2}{k}^{2}+{b}^{2}+{a}^{2}+{b}^{2}{k}^{2}}{{a}^{2}{b}^{2}(1+{k}^{2})}$=$\frac{{a}^{2}+{b}^{2}}{{a}^{2}{b}^{2}}$=$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$;
(2)O到直线PQ的距离d即为△POQ斜边上的高,
∴d=$\frac{|OP|•|OQ|}{|PQ|}$=$\sqrt{\frac{|OP{|}^{2}•|OQ{|}^{2}}{|PQ{|}^{2}}}$=$\sqrt{\frac{|OP{|}^{2}•|OQ{|}^{2}}{|OP{|}^{2}+|OQ{|}^{2}}}$=$\sqrt{\frac{{a}^{2}{b}^{2}}{{a}^{2}+{b}^{2}}}$(定值).
点评 本题考查椭圆的简单性质,涉及到两点间距离公式等基础知识,考查运算求解能力,注意解题方法的积累,属于中档题.

| A. | -5 | B. | 5 | C. | -10 | D. | 10 |
| A. | $\frac{5}{2}$ | B. | 4 | C. | $\frac{9}{2}$ | D. | 9 |
| A. | $\left\{\begin{array}{l}{a=\frac{2}{3}}\\{b=-3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=\frac{3}{2}}\\{b=-3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a=-\frac{3}{2}}\\{b=3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a=\frac{3}{2}}\\{b=3}\end{array}\right.$ |
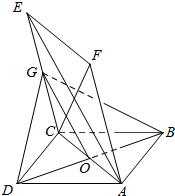 如图,已知边长为2的菱形ABCD与菱形ACEF全等,且∠FAC=∠ABC,平面ABCD⊥平面ACEF,点G为CE的中点.
如图,已知边长为2的菱形ABCD与菱形ACEF全等,且∠FAC=∠ABC,平面ABCD⊥平面ACEF,点G为CE的中点.