题目内容
4.已知函数f(x)=$\frac{{{e^x}-{e^{-x}}}}{2},g(x)=\frac{{{e^x}+{e^{-x}}}}{2}$(其中e=2.71718…),有下列命题:①f(x)是奇函数,g(x)是偶函数;
②对任意x∈R,都有f(2x)=f(x)•g(x);
③f(x)有零点,g(x)无零点.
其中正确的命题是①③.(填上所有正确命题的序号)
分析 直接由函数奇偶性的定义判断①正确;代值验证②错误;先判断函数单调性,g(x)有最小值;直接求出f(x)的零点,由单调性及奇偶性和最值说明g(x)无零点.
解答 解:f(-x)=$\frac{1}{2}$(e-x-ex)=-$\frac{1}{2}$(ex-e-x)=-f(x),故f(x)为奇函数,
g(-x)=$\frac{1}{2}$(e-x+ex)=g(x),故g(x)为偶函数,故命题①正确,
f(2x)=$\frac{1}{2}$(e2x-e-2x)=$\frac{1}{2}$(ex+e-x)(ex-e-x),
f(x)•g(x)=$\frac{1}{2}$(ex-e-x)$\frac{1}{2}$(e-x+ex)=$\frac{1}{4}$(ex+e-x)(ex-e-x),故命题②不正确;
函数y=ex,y=-e-x在实数集上均为增函数,
∴f(x)在R上单调递增,
设x1<x2<0,
则g(x1)-g(x2)=$\frac{1}{2}$(ex1+e-x1)-$\frac{1}{2}$(ex2+e-x2)=$\frac{1}{2}$[(ex1-ex2)+(1-$\frac{1}{{e}^{{x}_{1}}{e}^{{x}_{2}}}$)],
∵x1<x2<0,
∴g(x1)-g(x2)>0,即g(x1)>g(x2).
g(x)在(-∞,0)上单调递减,
当x=0时,g(x)有最小值1,且函数是偶函数,
∴g(x)无零点,
由f(x)=0,即$\frac{1}{2}$(ex-e-x)=0,得x=0,
∴f(x)有零点0,故命题③正确.
故答案为:①③.
点评 本题考查了命题的真假判断与应用,考查了函数的性质,是中档题.

练习册系列答案
相关题目
14.已知椭圆C1:$\frac{{x}^{2}}{{a}_{1}^2}$+$\frac{{y}^{2}}{{{b}_{1}}^{2}}$=1(a1>0,b2>0)与双曲线C2::$\frac{{x}^{2}}{{a}_{2}^2}$-$\frac{{y}^{2}}{{{b}_{2}}^{2}}$=1(a1>0,b2>0)有相同的焦点F1,F2,点P是两曲线的一个公共点,e1,e2又分别是两曲线的离心率,若PF1⊥PF2,则4e12+e22的最小值( )
| A. | $\frac{5}{2}$ | B. | 4 | C. | $\frac{9}{2}$ | D. | 9 |
15.已知直线l1,l2过椭圆$\frac{x^2}{4}$+$\frac{y^2}{{\frac{4}{3}}}$=1的中心且相互垂直的两条直线,分别交椭圆于A,B,C,D,四边形ABCD的面积的最小值是( )
| A. | 2 | B. | 4 | C. | $\frac{8\sqrt{3}}{3}$ | D. | $\frac{16\sqrt{3}}{3}$ |
13.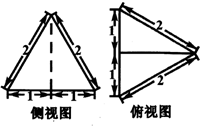 某三棱锥的侧视图,俯视图如图所示,则该三棱锥正视图的面积是( )
某三棱锥的侧视图,俯视图如图所示,则该三棱锥正视图的面积是( )
 某三棱锥的侧视图,俯视图如图所示,则该三棱锥正视图的面积是( )
某三棱锥的侧视图,俯视图如图所示,则该三棱锥正视图的面积是( )| A. | 2 | B. | 3 | C. | $\frac{3}{2}$ | D. | $\frac{5}{2}$ |
14.已知点P(x,y)是直线x+3y-2=0上的动点,则代数式2x+3×8y有( )
| A. | 最小值2$\sqrt{3}$ | B. | 最大值2$\sqrt{3}$ | C. | 最小值4$\sqrt{3}$ | D. | 最大值4$\sqrt{3}$ |
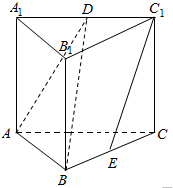 直三棱柱ABC-A1B1C1中,AA1=AC,AB⊥AC,D,E分别是A1C1,BC的中点.
直三棱柱ABC-A1B1C1中,AA1=AC,AB⊥AC,D,E分别是A1C1,BC的中点.