题目内容
1.已知等差数列{an}的前n项和为Sn,且a2=5,S9=99.(1)求an 及Sn;
(2)若数列{$\frac{4}{{{a}_{n}}^{2}-1}$}的前n项和Tn,试证明不等式$\frac{1}{2}$≤Tn<1成立.
分析 (1)设等差数列{an}的公差为d,运用通项公式和求和公式,列方程,即可解得首项和公差,进而得到通项和求和;
(2)化简数列bn=$\frac{4}{{{a}_{n}}^{2}-1}$=$\frac{1}{n}$-$\frac{1}{n+1}$,运用相互抵消求和可得Tn,再由数列的单调性和不等式的性质,即可得证.
解答 解:(1)设等差数列{an}的公差为d,
∵a2=5,S9=99.∴a1+d=5,9a1+$\frac{9×8}{2}$d=99,
解得a1=3,d=2,
∴an=3+2(n-1)=2n+1,Sn=3n+$\frac{1}{2}$n(n-1)•2=n2+2n;
(2)证明:设bn=$\frac{4}{{{a}_{n}}^{2}-1}$,∵an=2n+1,∴an2-1=4n(n+1),
∴bn=$\frac{4}{4n(n+1)}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,
即有Tn=b1+b2+b3+…+bn=(1-$\frac{1}{2}$)+($\frac{1}{2}-\frac{1}{3}$)+($\frac{1}{3}-\frac{1}{4}$)+…+($\frac{1}{n}$-$\frac{1}{n+1}$)
=1-$\frac{1}{n+1}$<1,
又Tn=1-$\frac{1}{n+1}$为递增数列,即有Tn≥T1=1-$\frac{1}{2}=\frac{1}{2}$,
综上所述:不等式$\frac{1}{2}$≤Tn<1成立.
点评 本题考查等差数列的通项公式和求和公式的运用,同时考查数列的求和方法:裂项相消求和,考查运算能力,属于中档题.

练习册系列答案
相关题目
11.两直线ax+by+4=0和(1-a)x-y-b=O都平行于x+2y+3=0,则( )
| A. | $\left\{\begin{array}{l}{a=\frac{2}{3}}\\{b=-3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=\frac{3}{2}}\\{b=-3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a=-\frac{3}{2}}\\{b=3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a=\frac{3}{2}}\\{b=3}\end{array}\right.$ |
6.下列函数中,是偶函数且在(0,1)上单调递减的是( )
| A. | y=x-2 | B. | y=x4 | C. | y=${x^{\frac{1}{2}}}$ | D. | y=-${x^{\frac{1}{3}}}$ |
13.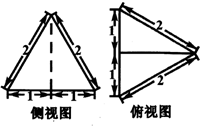 某三棱锥的侧视图,俯视图如图所示,则该三棱锥正视图的面积是( )
某三棱锥的侧视图,俯视图如图所示,则该三棱锥正视图的面积是( )
 某三棱锥的侧视图,俯视图如图所示,则该三棱锥正视图的面积是( )
某三棱锥的侧视图,俯视图如图所示,则该三棱锥正视图的面积是( )| A. | 2 | B. | 3 | C. | $\frac{3}{2}$ | D. | $\frac{5}{2}$ |
10.将函数f(x)=sin(2x-$\frac{π}{6}$)的图象上所有的点向左平移$\frac{π}{3}$个单位(纵坐标不变),则所得图象的解析式是( )
| A. | y=-cos2x | B. | y=cos2x | C. | y=sin(2x-$\frac{5π}{6}$) | D. | y=sin(2x+$\frac{π}{6}$) |
11.过双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点F作圆x2+y2=a2的切线,交y轴于点P,若|OF|=2|OP|,则双曲线C的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
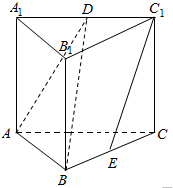 直三棱柱ABC-A1B1C1中,AA1=AC,AB⊥AC,D,E分别是A1C1,BC的中点.
直三棱柱ABC-A1B1C1中,AA1=AC,AB⊥AC,D,E分别是A1C1,BC的中点.