题目内容
20.已知F1(-c,0),F2(c,0)分别是椭圆M:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点,且|F1F2|=2$\sqrt{3}$,离心率e=$\frac{\sqrt{3}}{2}$.(1)求椭圆M的标准方程;
(2)过椭圆右焦点F2作直线l交椭圆M于A,B两点.
①当直线l的斜率为1时,求线段AB的长;
②若椭圆M上存在点P,使得以OA,OB为邻边的四边形OAPB为平行四边形(O为坐标原点),求直线l的方程.
分析 (1)运用离心率公式和a,b,c的关系,可得a,b,进而得到椭圆方程;
(2)①设直线l:y=x-$\sqrt{3}$,代入椭圆方程,求出方程的根,即可求线段AB的长;
②假设椭圆上存在点P(m,n),使得以OA、OB为邻边的四边形OAPB为平行四边形.设直线方程为y=k(x-$\sqrt{3}$),代入椭圆方程,运用韦达定理,结合$\overrightarrow{OP}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$,则m=x1+x2,n=y1+y2,求得P的坐标,代入椭圆方程,即可得到k,即可判断P的存在和直线的方程.
解答 解:(1)由题意,c=$\sqrt{3}$,$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,
∴a=2,b=1,
∴椭圆M的标准方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$;
(2)①可设直线方程为y=x-$\sqrt{3}$
代入椭圆方程可得5x2-8$\sqrt{3}$x+8=0
∴x=$\frac{4\sqrt{3}±2\sqrt{2}}{5}$
∴弦AB的长为$\sqrt{2}×\frac{4\sqrt{2}}{5}$=$\frac{8}{5}$;
②假设椭圆上存在点P(m,n),使得以OA、OB为邻边的四边形OAPB为平行四边形.
设直线方程为y=k(x-$\sqrt{3}$),代入椭圆方程,可得(1+4k2)x2-8$\sqrt{3}$k2x+12k2-4=0,
设A(x1,y1),B(x2,y2),
由$\overrightarrow{OP}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$,则m=x1+x2,n=y1+y2,
x1+x2=$\frac{8\sqrt{3}{k}^{2}}{1+4{k}^{2}}$,x1x2=$\frac{12{k}^{2}-4}{1+4{k}^{2}}$,
y1+y2=k(x1+x2-2$\sqrt{3}$)=k($\frac{8\sqrt{3}{k}^{2}}{1+4{k}^{2}}$-2$\sqrt{3}$)=$\frac{-2\sqrt{3}k}{1+4{k}^{2}}$,
即有P($\frac{8\sqrt{3}{k}^{2}}{1+4{k}^{2}}$,$\frac{-2\sqrt{3}k}{1+4{k}^{2}}$),
代入椭圆方程可得$\frac{48{k}^{4}}{(1+4{k}^{2})^{2}}+\frac{12{k}^{2}}{(1+4{k}^{2})^{2}}$=1,
解得k2=$\frac{1}{8}$,解得k=±$\frac{\sqrt{2}}{4}$,
故存在点P($\frac{\sqrt{3}}{3}$,-$\frac{\sqrt{6}}{6}$),或($\frac{\sqrt{3}}{3}$,-$\frac{\sqrt{6}}{6}$),
则有直线l:y=$\frac{\sqrt{2}}{4}$x-$\frac{\sqrt{6}}{4}$或y=-$\frac{\sqrt{2}}{4}$x+$\frac{\sqrt{6}}{4}$.
点评 本题考查椭圆的方程和性质,主要考查离心率公式和方程的运用,联立直线方程,运用韦达定理,考查运算能力,属于中档题.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案| A. | $\left\{\begin{array}{l}{a=\frac{2}{3}}\\{b=-3}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=\frac{3}{2}}\\{b=-3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a=-\frac{3}{2}}\\{b=3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a=\frac{3}{2}}\\{b=3}\end{array}\right.$ |
| A. | 2 | B. | 4 | C. | $\frac{8\sqrt{3}}{3}$ | D. | $\frac{16\sqrt{3}}{3}$ |
| A. | 45 | B. | 9 | C. | -45 | D. | -9 |
| A. | y=-cos2x | B. | y=cos2x | C. | y=sin(2x-$\frac{5π}{6}$) | D. | y=sin(2x+$\frac{π}{6}$) |
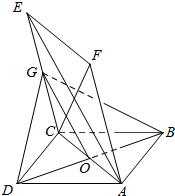 如图,已知边长为2的菱形ABCD与菱形ACEF全等,且∠FAC=∠ABC,平面ABCD⊥平面ACEF,点G为CE的中点.
如图,已知边长为2的菱形ABCD与菱形ACEF全等,且∠FAC=∠ABC,平面ABCD⊥平面ACEF,点G为CE的中点.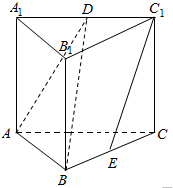 直三棱柱ABC-A1B1C1中,AA1=AC,AB⊥AC,D,E分别是A1C1,BC的中点.
直三棱柱ABC-A1B1C1中,AA1=AC,AB⊥AC,D,E分别是A1C1,BC的中点.