题目内容
18.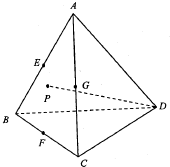 如图E、F、G分别是各棱长均相等的三棱锥A-BCD的棱AB、BC、AC的中点,点P在侧面ABC及其边界上运动,DP⊥AB,则动点P的轨迹是( )
如图E、F、G分别是各棱长均相等的三棱锥A-BCD的棱AB、BC、AC的中点,点P在侧面ABC及其边界上运动,DP⊥AB,则动点P的轨迹是( )| A. | 线段FG | B. | 线段EG | C. | 线段EF | D. | 线段EC |
分析 确定DA在侧面ABC上的射影为CE,CE⊥AB,根据CP⊥AB,即可得出结论.
解答 解:因为E是各棱长均相等的三棱锥A-BCD的棱AB的中点,
所以DA在侧面ABC上的射影为CE,CE⊥AB,
因为点P在侧面ABC及其边界上运动,DP⊥AB,
所以动点P的轨迹是线段EC,
故选:D.
点评 本题考查轨迹方程,考查学生分析解决问题的能力,确定CE⊥AB是关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
6.下列函数中,是偶函数且在(0,1)上单调递减的是( )
| A. | y=x-2 | B. | y=x4 | C. | y=${x^{\frac{1}{2}}}$ | D. | y=-${x^{\frac{1}{3}}}$ |
13.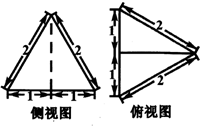 某三棱锥的侧视图,俯视图如图所示,则该三棱锥正视图的面积是( )
某三棱锥的侧视图,俯视图如图所示,则该三棱锥正视图的面积是( )
 某三棱锥的侧视图,俯视图如图所示,则该三棱锥正视图的面积是( )
某三棱锥的侧视图,俯视图如图所示,则该三棱锥正视图的面积是( )| A. | 2 | B. | 3 | C. | $\frac{3}{2}$ | D. | $\frac{5}{2}$ |
3.下列函数中,图象不关于原点对称的是( )
| A. | y=ex-e-x | B. | y=$\frac{2}{{{e^x}+1}}$-1 | C. | $y=ln(x+\sqrt{{x^2}+1})$ | D. | y=lnsinx |
10.将函数f(x)=sin(2x-$\frac{π}{6}$)的图象上所有的点向左平移$\frac{π}{3}$个单位(纵坐标不变),则所得图象的解析式是( )
| A. | y=-cos2x | B. | y=cos2x | C. | y=sin(2x-$\frac{5π}{6}$) | D. | y=sin(2x+$\frac{π}{6}$) |
7.已知各项均为正数的等比数列{an}中,a2=1,则其前3项的和S3的取值范围是( )
| A. | (1,+∞) | B. | (0,2] | C. | (0,3] | D. | [3,+∞) |
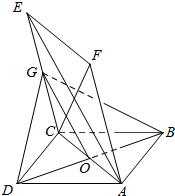 如图,已知边长为2的菱形ABCD与菱形ACEF全等,且∠FAC=∠ABC,平面ABCD⊥平面ACEF,点G为CE的中点.
如图,已知边长为2的菱形ABCD与菱形ACEF全等,且∠FAC=∠ABC,平面ABCD⊥平面ACEF,点G为CE的中点. 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的面积为πab,随机向矩形区域内投掷一飞镖,则飞镖落入椭圆区域内的概率是$\frac{π}{4}$.
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的面积为πab,随机向矩形区域内投掷一飞镖,则飞镖落入椭圆区域内的概率是$\frac{π}{4}$.