题目内容
1.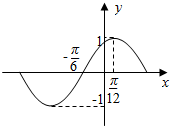 函数y=f(x)的部分图象如图所示,函数g(x)=sin(2x+φ)(0<φ<π)为偶函数,要得到g(x)的图象,只需将y=f(x)的图象向( )平移( )个单位.
函数y=f(x)的部分图象如图所示,函数g(x)=sin(2x+φ)(0<φ<π)为偶函数,要得到g(x)的图象,只需将y=f(x)的图象向( )平移( )个单位.| A. | 右:$\frac{π}{6}$ | B. | 左:$\frac{π}{6}$ | C. | 右:$\frac{π}{12}$ | D. | 左:$\frac{π}{12}$ |
分析 由函数的最值求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的f(x)的解析式.求得g(x)后再根据函数y=Asin(ωx+φ)的图象的变换规律,可得结论.
解答 解:由函数f(x)=Asin(ωx+φ)的图象可得:
A=1,T=$\frac{2π}{ω}$=4($\frac{π}{12}$+$\frac{π}{6}$)=π,∴ω=2.
再由五点法作图可得 2×(-$\frac{π}{6}$)+φ=0,∴φ=$\frac{π}{3}$.
故函数的f(x)的解析式为 f(x)=sin(2x+$\frac{π}{3}$)=sin2(x+$\frac{π}{6}$).
∵g(x)=sin(2x+φ)(0<φ<π)为偶函数,
∴φ=$\frac{π}{2}$,g(x)=sin(2x+$\frac{π}{2}$)=sin2(x+$\frac{π}{4}$),
故把f(x)=sin2(x+$\frac{π}{6}$)的图象向左平移$\frac{π}{12}$个单位长度,可得g(x)=sin(2x+$\frac{π}{2}$)的图象.
故选:D.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,函数y=Asin(ωx+φ)的图象的变换规律,属于中档题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
相关题目
12.如果等差数列中a3=8,则S5=( )
| A. | 20 | B. | 30 | C. | 40 | D. | 16 |
9.已知-1<α<0,则( )
| A. | ${0.2^α}>{(\frac{1}{2})^α}>{2^α}$ | B. | ${2^α}>{0.2^α}>{(\frac{1}{2})^α}$ | C. | ${(\frac{1}{2})^α}>{0.2^α}>{2^α}$ | D. | ${2^α}>{(\frac{1}{2})^α}>{0.2^α}$ |
6.从装有2个红球和2个黑球的口袋内任取2个球,那么互斥而不对立的两个事件是( )
| A. | 恰有1个黑球与恰有2个黑球 | B. | 至少有一个黑球与都是黑球 | ||
| C. | 至少有一个黑球与至少有1个红球 | D. | 至多有一个黑球与都是黑球 |
13.县政府组织500人参加卫生城市创建“义工”活动,按年龄分组所得频率分布直方图如下图,完成下列问题:
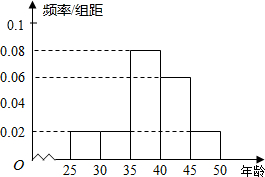
(1)如表是年龄的频数分布表,求出表中正整数a、b的值;
(2)现在要从年龄较小的第1、2、3组中用分层抽样的方法抽取6人,则年龄在第1、2、3组的各抽取多少人?
(3)在第(2)问的前提下,从这6人中随机抽取2人参加社区活动,求至少有1人年龄在第3组的概率.

| 组别 | [25,30) | [30,35) | [35,40) | [40,45) | [45,50) |
| 人数 | 50 | 50 | a | 150 | b |
(2)现在要从年龄较小的第1、2、3组中用分层抽样的方法抽取6人,则年龄在第1、2、3组的各抽取多少人?
(3)在第(2)问的前提下,从这6人中随机抽取2人参加社区活动,求至少有1人年龄在第3组的概率.
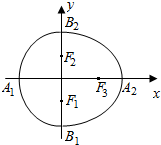 我们把由半椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)与半椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x<0)合成的曲线称作“果圆”(其中a2=b2+c2,a>b>c>0).如图,设点F0,F1,F2是相应椭圆的焦点,A1、A2和B1、B2是“果圆”与x,y轴的交点,若△F0F1F2是边长为1的等边三角形,则a,b的值分别为( )
我们把由半椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)与半椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x<0)合成的曲线称作“果圆”(其中a2=b2+c2,a>b>c>0).如图,设点F0,F1,F2是相应椭圆的焦点,A1、A2和B1、B2是“果圆”与x,y轴的交点,若△F0F1F2是边长为1的等边三角形,则a,b的值分别为( )