题目内容
11.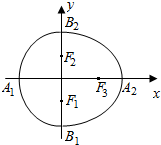 我们把由半椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)与半椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x<0)合成的曲线称作“果圆”(其中a2=b2+c2,a>b>c>0).如图,设点F0,F1,F2是相应椭圆的焦点,A1、A2和B1、B2是“果圆”与x,y轴的交点,若△F0F1F2是边长为1的等边三角形,则a,b的值分别为( )
我们把由半椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x≥0)与半椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x<0)合成的曲线称作“果圆”(其中a2=b2+c2,a>b>c>0).如图,设点F0,F1,F2是相应椭圆的焦点,A1、A2和B1、B2是“果圆”与x,y轴的交点,若△F0F1F2是边长为1的等边三角形,则a,b的值分别为( )| A. | 5,4 | B. | $\sqrt{3}$,1 | C. | 5,3 | D. | $\frac{\sqrt{7}}{2}$,1 |
分析 由题意可知c=$\sqrt{3}$|OF2|求得c,再由|OF2|=$\sqrt{{b}^{2}-{c}^{2}}$=$\frac{1}{2}$,解得b,最后由a2=b2+c2求得a.
解答 解:由题意可得|OF2|=$\sqrt{{b}^{2}-{c}^{2}}$=$\frac{1}{2}$,
|OF0|=c=$\sqrt{3}$|OF2|=$\frac{\sqrt{3}}{2}$,解得b=1,
又a2=b2+c2=1+$\frac{3}{4}$=$\frac{7}{4}$,得a=$\frac{\sqrt{7}}{2}$,即a=$\frac{\sqrt{7}}{2}$,b=1.
故选:D.
点评 本题主要考查新定义的理解和运用,考查椭圆的方程和性质.考查运算能力,属基础题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
1.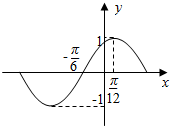 函数y=f(x)的部分图象如图所示,函数g(x)=sin(2x+φ)(0<φ<π)为偶函数,要得到g(x)的图象,只需将y=f(x)的图象向( )平移( )个单位.
函数y=f(x)的部分图象如图所示,函数g(x)=sin(2x+φ)(0<φ<π)为偶函数,要得到g(x)的图象,只需将y=f(x)的图象向( )平移( )个单位.
 函数y=f(x)的部分图象如图所示,函数g(x)=sin(2x+φ)(0<φ<π)为偶函数,要得到g(x)的图象,只需将y=f(x)的图象向( )平移( )个单位.
函数y=f(x)的部分图象如图所示,函数g(x)=sin(2x+φ)(0<φ<π)为偶函数,要得到g(x)的图象,只需将y=f(x)的图象向( )平移( )个单位.| A. | 右:$\frac{π}{6}$ | B. | 左:$\frac{π}{6}$ | C. | 右:$\frac{π}{12}$ | D. | 左:$\frac{π}{12}$ |
6.若集合A={(x,y)|x2+y2≤16},B={(x,y)|x2+(y-2)2≤a-1},(a>1),且A∩B=B,则a的取值范围是( )
| A. | 1<a<5 | B. | a≥5 | C. | 1<a≤5 | D. | a<5 |
3.已知A,B,C,D是空间不共面四点.且满足AB=CD,AC=BD,AD=BC,则△BCD是( )
| A. | 钝角三角形 | B. | 直角三角形 | C. | 锐角三角形 | D. | 不确定 |