题目内容
6．从装有2个红球和2个黑球的口袋内任取2个球，那么互斥而不对立的两个事件是（ ）| A． | 恰有1个黑球与恰有2个黑球 | B． | 至少有一个黑球与都是黑球 | ||
| C． | 至少有一个黑球与至少有1个红球 | D． | 至多有一个黑球与都是黑球 |
分析 依据互斥事件与对立事件的定义，以及它们的关系，判断．
解答 解：从装有2个红球和2个黑球的口袋中任取2个球，包括3种情况：①恰有一个黑球，②恰有两个黑球，③没有黑球．
故恰有一个黑球与恰有两个黑球不可能同时发生，它们是互斥事件，再由这两件事的和不是必然事件，故他们是互斥但不对立的事件，
故选：A．
点评 本题主要考查互斥事件与对立事件的定义，以及它们的关系，属于基础题．
练习册系列答案
相关题目
1．
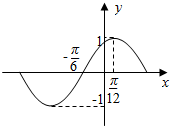函数y=f（x）的部分图象如图所示，函数g（x）=sin（2x+φ）（0＜φ＜π）为偶函数，要得到g（x）的图象，只需将y=f（x）的图象向（ ）平移（ ）个单位．
函数y=f（x）的部分图象如图所示，函数g（x）=sin（2x+φ）（0＜φ＜π）为偶函数，要得到g（x）的图象，只需将y=f（x）的图象向（ ）平移（ ）个单位．| A． | 右：$\frac{π}{6}$ | B． | 左：$\frac{π}{6}$ | C． | 右：$\frac{π}{12}$ | D． | 左：$\frac{π}{12}$ |
18．在△ABC中，a=1，b=6，C=60°，则三角形的面积为（ ）
| A． | $\frac{3}{2}$ | B． | $\frac{3\sqrt{3}}{2}$ | C． | 3$\sqrt{3}$ | D． | 3 |