题目内容
10．已知x＞0，y＞0，$\frac{1}{x}+\frac{1}{y}$=2，若x+y＞3m2+m恒成立，则实数m的取值范围用区间表示为（-1，$\frac{2}{3}$）．分析 首先，根据已知条件，转化为（x+y）min＞3m2+m，然后得到x+y=$\frac{1}{2}$×2×（x+y）=$\frac{1}{2}$（x+y）（$\frac{1}{x}$+$\frac{1}{y}$），再结合基本不等式确定其最值即可．
解答 解：∵x＞0，y＞0，x+y＞3m2+m恒成立，
∴（x+y）min＞3m2+m，
∵x+y=$\frac{1}{2}$×2×（x+y）
=$\frac{1}{2}$（x+y）（$\frac{1}{x}$+$\frac{1}{y}$）
=$\frac{1}{2}$（2+$\frac{y}{x}$+$\frac{x}{y}$）≥$\frac{1}{2}$（2+2）=2，
∴3m2+m＜2，
∴-1＜m＜$\frac{2}{3}$．
故答案为：（-1，$\frac{2}{3}$）．
点评 本题重点考查了基本不等式及其灵活运用，注意基本不等式的适应关键：一正、二定（定值）、三相等（即验证等号成立的条件），注意给条件求最值问题，一定要充分利用所给的条件，作出适当的变形，然后，巧妙的利用基本不等式进行处理，这也是近几年常考题目，复习时需要引起高度关注．
练习册系列答案
相关题目
20．某设备的使用年限x和维修费用y（万元）有如下统计数据
（1）请根据上表提供的数据，求出y与x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$
（2）试估计当使用年限为10年时，维修费用是多少？
（参考数据$\left\{\begin{array}{l}{\widehat{b}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}}\\{\widehat{a}=\overline{y}-\widehat{b}\overline{x}}\end{array}\right.$，其中（$\overline{x}$，$\overline{y}$）为样本中心．
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
（2）试估计当使用年限为10年时，维修费用是多少？
（参考数据$\left\{\begin{array}{l}{\widehat{b}=\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}}\\{\widehat{a}=\overline{y}-\widehat{b}\overline{x}}\end{array}\right.$，其中（$\overline{x}$，$\overline{y}$）为样本中心．
1．
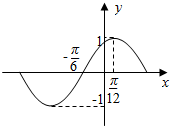函数y=f（x）的部分图象如图所示，函数g（x）=sin（2x+φ）（0＜φ＜π）为偶函数，要得到g（x）的图象，只需将y=f（x）的图象向（ ）平移（ ）个单位．
函数y=f（x）的部分图象如图所示，函数g（x）=sin（2x+φ）（0＜φ＜π）为偶函数，要得到g（x）的图象，只需将y=f（x）的图象向（ ）平移（ ）个单位．| A． | 右：$\frac{π}{6}$ | B． | 左：$\frac{π}{6}$ | C． | 右：$\frac{π}{12}$ | D． | 左：$\frac{π}{12}$ |
18．在△ABC中，a=1，b=6，C=60°，则三角形的面积为（ ）
| A． | $\frac{3}{2}$ | B． | $\frac{3\sqrt{3}}{2}$ | C． | 3$\sqrt{3}$ | D． | 3 |
5．下列各函数中，最小值为4的是（ ）
| A． | y=x+$\frac{4}{x}$ | B． | y=sinx+$\frac{4}{sinx}$，x∈（0，$\frac{π}{2}$） | ||
| C． | y=$\frac{{x}^{2}+2}{\sqrt{{x}^{2}+1}}$ | D． | y=$\sqrt{x}$+$\frac{9}{\sqrt{x}}$-2 |