题目内容
若点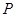 在椭圆
在椭圆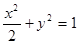 上,
上,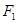 、
、 分别是椭圆的两焦点,且
分别是椭圆的两焦点,且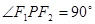 ,则
,则 的面积是 ( )
的面积是 ( )
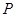 在椭圆
在椭圆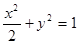 上,
上,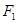 、
、 分别是椭圆的两焦点,且
分别是椭圆的两焦点,且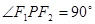 ,则
,则 的面积是 ( )
的面积是 ( )| A.2 | B.1 | C.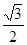 | D.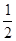 |
B
分析:由椭圆的定义可得 m+n="2a=2"
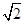 ①,Rt△F1PF2中,由勾股定理可得m
①,Rt△F1PF2中,由勾股定理可得m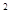 +n
+n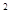 =4②,由①②可得m?n的值,利用△F1PF2的面积是
=4②,由①②可得m?n的值,利用△F1PF2的面积是 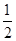 m?n求得结果.
m?n求得结果.解答:解:由椭圆的方程可得 a=
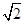 ,b=1,c=1,令|F
,b=1,c=1,令|F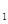 P|=m、|PF
P|=m、|PF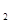 |=n,
|=n,由椭圆的定义可得 m+n=2a=2
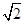 ①,Rt△F
①,Rt△F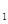 PF
PF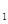 中,
中,由勾股定理可得(2c)
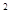 =m
=m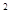 +n
+n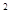 ,m
,m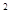 +n
+n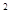 =4②,由①②可得m?n=2,
=4②,由①②可得m?n=2,∴△F
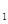 PF
PF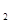 的面积是
的面积是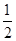 m?n=1,
m?n=1,故选B.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
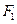 、
、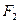 在x轴上,点P为椭圆上的一个动点,且
在x轴上,点P为椭圆上的一个动点,且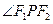 的最大值为90°,直线l过左焦点
的最大值为90°,直线l过左焦点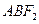 的面积最大值为12.
的面积最大值为12.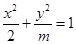 的离心率为
的离心率为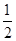 , 则m的值为( )
, 则m的值为( )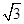
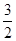
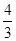
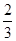
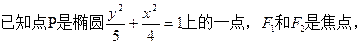
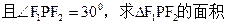 .
.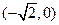 ,
,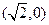 ,离心率是
,离心率是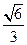 ,直线
,直线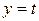 椭圆C交与不同的两点M,N,以线段MN为直径作圆P,圆心为P。
椭圆C交与不同的两点M,N,以线段MN为直径作圆P,圆心为P。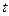 的值;
的值;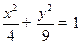 的上、下两个焦点分别为
的上、下两个焦点分别为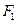 、
、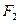 ,点
,点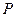 为该椭圆上一点,若
为该椭圆上一点,若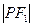 、
、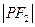 为方程
为方程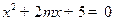 的两根,则
的两根,则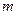 =" " .
=" " .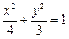 ,则直线
,则直线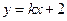 与椭圆至多有一个公共点的充要条件
与椭圆至多有一个公共点的充要条件 )且离心率为
)且离心率为 的椭圆中心在原点,x轴上的两焦点分别为F1,F2,过F1作直线交椭圆于A,B两点,则△ABF2的周长为____
的椭圆中心在原点,x轴上的两焦点分别为F1,F2,过F1作直线交椭圆于A,B两点,则△ABF2的周长为____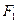 (-3,0),
(-3,0),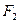 (3,0),点M满足
(3,0),点M满足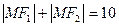 ,则M的轨迹方程为 ▲
,则M的轨迹方程为 ▲