题目内容
本题满分14分)已知椭圆C的中心在原点,焦点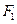 、
、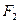 在x轴上,点P为椭圆上的一个动点,且
在x轴上,点P为椭圆上的一个动点,且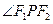 的最大值为90°,直线l过左焦点
的最大值为90°,直线l过左焦点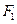 与椭圆交于A、B两点,
与椭圆交于A、B两点,
△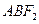 的面积最大值为12.
的面积最大值为12.
(1)求椭圆C的离心率;(5分)
(2)求椭圆C的方程。(9分)
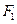 、
、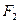 在x轴上,点P为椭圆上的一个动点,且
在x轴上,点P为椭圆上的一个动点,且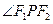 的最大值为90°,直线l过左焦点
的最大值为90°,直线l过左焦点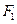 与椭圆交于A、B两点,
与椭圆交于A、B两点,△
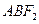 的面积最大值为12.
的面积最大值为12.(1)求椭圆C的离心率;(5分)
(2)求椭圆C的方程。(9分)
(1)
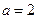 ,
,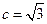
(2)
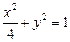
解:(1)根据椭圆的定义,可知动点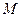 的轨迹为椭圆,设椭圆方程:
的轨迹为椭圆,设椭圆方程: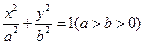 其焦距为
其焦距为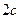 ,则
,则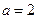 ,
,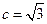 ,则
,则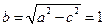 .
.
所以动点M的轨迹方程为: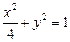 . ………………………5分
. ………………………5分
(2)当直线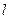 的斜率不存在时,不满足题意.
的斜率不存在时,不满足题意.
当直线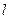 的斜率存在时,设直线
的斜率存在时,设直线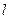 的方程为
的方程为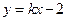 ,设
,设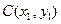 ,
,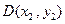 ,
,
∵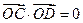 ,∴
,∴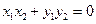 . ………………………6分
. ………………………6分
∵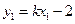 ,
,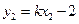 , ∴
, ∴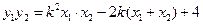 .
.
∴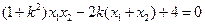 .(1) ………………………8分
.(1) ………………………8分
由方程组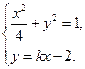 得.
得. 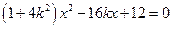
由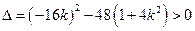 得
得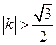
则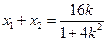 ,
,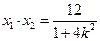 , ………………………11分
, ………………………11分
代入①,得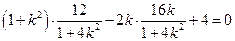 .
.
即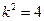 ,解得,
,解得,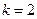 或
或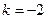 . 经验证
. 经验证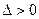 。 ………………………13分
。 ………………………13分
所以,直线 的方程是
的方程是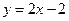 或
或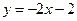 . ………………………14分
. ………………………14分
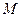 的轨迹为椭圆,设椭圆方程:
的轨迹为椭圆,设椭圆方程: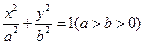 其焦距为
其焦距为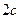 ,则
,则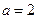 ,
,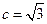 ,则
,则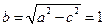 .
.所以动点M的轨迹方程为:
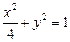 . ………………………5分
. ………………………5分(2)当直线
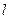 的斜率不存在时,不满足题意.
的斜率不存在时,不满足题意.当直线
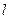 的斜率存在时,设直线
的斜率存在时,设直线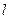 的方程为
的方程为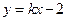 ,设
,设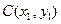 ,
,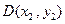 ,
,∵
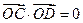 ,∴
,∴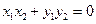 . ………………………6分
. ………………………6分∵
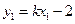 ,
,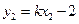 , ∴
, ∴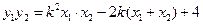 .
.∴
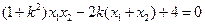 .(1) ………………………8分
.(1) ………………………8分由方程组
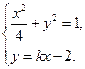 得.
得. 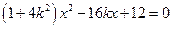
由
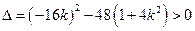 得
得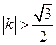
则
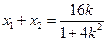 ,
,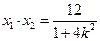 , ………………………11分
, ………………………11分代入①,得
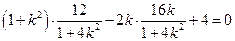 .
.即
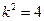 ,解得,
,解得,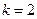 或
或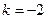 . 经验证
. 经验证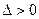 。 ………………………13分
。 ………………………13分所以,直线
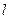 的方程是
的方程是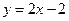 或
或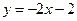 . ………………………14分
. ………………………14分
练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
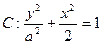
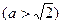 的离心率为
的离心率为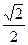 ,其两焦点分别为
,其两焦点分别为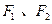 ,
,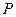 是椭圆在第一象限弧上一点,并满足
是椭圆在第一象限弧上一点,并满足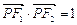 ,过
,过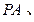
 分别交椭圆于
分别交椭圆于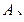
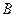 两点.
两点. 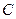
 的方程.
的方程.
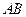 的方程.
的方程. 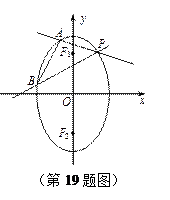
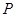 在椭圆
在椭圆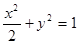 上,
上,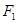 、
、 分别是椭圆的两焦点,且
分别是椭圆的两焦点,且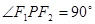 ,则
,则 的面积是 ( )
的面积是 ( )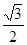
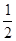
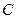 :
: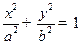
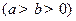 的左、右焦点分别为
的左、右焦点分别为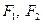 ,上顶点为
,上顶点为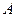 ,过点
,过点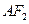 垂直的直线交
垂直的直线交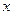 轴负半轴于点
轴负半轴于点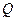 ,且
,且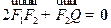 ,若过
,若过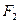 三点的圆恰好与直线
三点的圆恰好与直线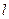 :
: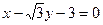 相切. 过定点
相切. 过定点 的直线
的直线 与椭圆
与椭圆 ,
, 两点(点
两点(点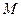 ,
,
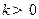 ,在
,在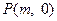 ,使得以
,使得以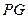 ,
,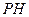 为邻边的平行四边形是菱形. 如果存在,求出
为邻边的平行四边形是菱形. 如果存在,求出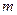 的取值范围,如果不存在,请说明理由;
的取值范围,如果不存在,请说明理由;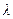 满足
满足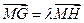 ,求
,求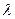 的取值范围.
的取值范围.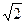 ),且过点
),且过点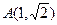 ,过A作倾斜角互补的两条直线,它们与椭圆的另一个交点分别为点B和点C。
,过A作倾斜角互补的两条直线,它们与椭圆的另一个交点分别为点B和点C。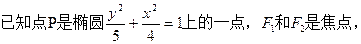
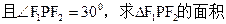 .
. 分别在图中抛物线
分别在图中抛物线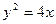 及椭圆
及椭圆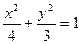 的实线上运动,若
的实线上运动,若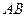 ∥
∥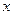 轴,点
轴,点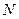 的坐标为
的坐标为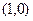 ,则
,则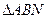 的周长
的周长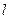 的取值范围是 ▲ .
的取值范围是 ▲ .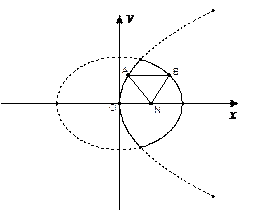
 分15分)
分15分) 知椭圆
知椭圆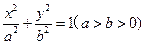 的离心率
的离心率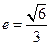 ,过点
,过点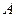
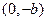 和
和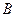
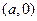 的直线与原点的距离为
的直线与原点的距离为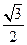 .
. 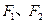 为椭圆的左、右焦点,过
为椭圆的左、右焦点,过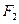 作直线交椭圆于
作直线交椭圆于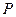
 、
、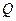 两点,求
两点,求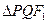 的内切圆半径
的内切圆半径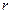 的最大值.
的最大值.
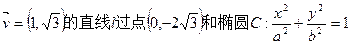
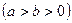 的右焦点,且椭圆的离心率为
的右焦点,且椭圆的离心率为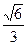 .
.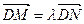 ,
,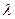 的取值范围.
的取值范围.