题目内容
【题目】已知曲线![]() 在点
在点![]() 处的切线与曲线
处的切线与曲线![]() 也相切.
也相切.
(1)求实数![]() 的值;
的值;
(2)设函数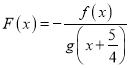 ,若
,若![]() 且
且![]() ,证明:
,证明: ![]() .
.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】试题分析:(1)根据导数的几何意义得到![]() ,先求出
,先求出![]() 在
在![]() 处的切线方程是
处的切线方程是![]() ,再根据题意这个直线也是
,再根据题意这个直线也是![]() 的切线,联立判别式等于零解出参数即可;(2)研究函数的单调性得到当
的切线,联立判别式等于零解出参数即可;(2)研究函数的单调性得到当![]() 时,
时, ![]() 是减函数;当
是减函数;当![]() 时,
时, ![]() 是增函数,再证当
是增函数,再证当![]() 时,
时, ![]()
![]() 恒成立,即
恒成立,即![]() ,赋值法得到
,赋值法得到![]() ,证得即可。
,证得即可。
(1) ∵![]() ,当
,当![]() 时,
时, ![]() ,故
,故![]() 在
在![]() 处的切线方程是
处的切线方程是![]() ,联立
,联立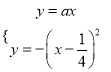 ,消去
,消去![]() 得
得![]() ,∴
,∴![]() ,∴
,∴![]() 或1,故
或1,故![]() .
.
(2)由(1)知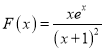 ,由
,由![]() ,则
,则![]() .又
.又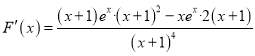
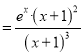 ,当
,当![]() 时,
时, ![]() 是减函数;当
是减函数;当![]() 时,
时, ![]() 是增函数,令
是增函数,令![]() ,
, ![]()
![]()
![]() ,再令
,再令![]() ,则
,则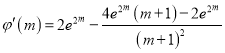
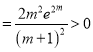 ,∴
,∴![]() .又
.又![]() ,当
,当![]() 时,
时, ![]()
![]() 恒成立,即
恒成立,即![]() 恒成立.令
恒成立.令![]() ,即
,即![]() ,有
,有![]() ,即
,即![]() ,∵
,∵![]() ,∴
,∴![]() .又
.又![]() ,必有
,必有![]() ,又当
,又当![]() 时,
时, ![]() 是增函数, ∴-
是增函数, ∴-![]() ,即
,即![]() .
.

练习册系列答案
相关题目