题目内容
【题目】某学校对高三学生一次模拟考试的数学成绩进行分析,随机抽取了部分学生的成绩,得到如图所示的成绩频率分布直方图.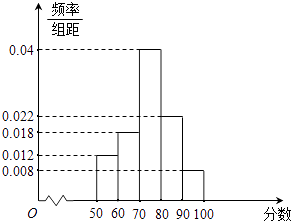
(1)根据频率分布直方图估计这次考试全校学生数学成绩的众数、中位数和平均值;
(2)若成绩不低于80分为优秀成绩,视频率为概率,从全校学生中有放回的任选3名学生,用变量ξ表示3名学生中获得优秀成绩的人数,求变量ξ的分布列及数学期望E(ξ).
【答案】
(1)解:由频率分布直方图得[70,80)对应的小矩形最高,
∴众数为: ![]() =75,
=75,
∵[50,70)的频率为(0.012+0.018)×10=0.3,
[70,80)的频率为0.04×10=0.4,
∴中位数为:70+ ![]() =75,
=75,
平均值为:55×0.12+65×0.18+75×0.40+85×0.22+95×0.08=74.6
所以综合素质成绩的平均值为74.6.
(2)解:由频率分布直方图知优秀率为10×(0.008+0.022)=0.3,
由题意知ξ~B(3,0.3), ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
故ξ的分布列为
P | 0 | 1 | 2 | 3 |
ξ | 0.343 | 0.441 | 0.189 | 0.027 |
E(ξ)=0×0.343+1×0.441+2×0.189+3×0.027=0.9.
【解析】(1)由频率分布直方图得[70,80)对应的小矩形最高,能出众数,由频率分布直方图的性质能求出中位数和综合素质成绩的平均值.(2)由频率分布直方图知优秀率为0.3,由题意知ξ~B(3,0.3),由此能求出ξ的分布列和E(ξ).
【考点精析】根据题目的已知条件,利用平均数、中位数、众数和离散型随机变量及其分布列的相关知识可以得到问题的答案,需要掌握⑴平均数、众数和中位数都是描述一组数据集中趋势的量;⑵平均数、众数和中位数都有单位;⑶平均数反映一组数据的平均水平,与这组数据中的每个数都有关系,所以最为重要,应用最广;⑷中位数不受个别偏大或偏小数据的影响;⑸众数与各组数据出现的频数有关,不受个别数据的影响,有时是我们最为关心的数据;在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案