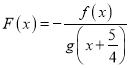题目内容
【题目】已知函数 
，函数 
x．
（1）若g（mx2+2x+m）的定义域为R，求实数m的取值范围；
（2）当x∈[﹣1，1]时，求函数y=[f（x）]2﹣2af（x）+3的最小值h（a）；
（3）是否存在非负实数m、n，使得函数 
的定义域为[m，n]，值域为[2m，2n]，若存在，求出m、n的值；若不存在，则说明理由．
【答案】
（1）
解：∵ 
，
∴ 
，
令u=mx2+2x+m，则 
，
当m=0时，u=2x， 
的定义域为（0，+∞），不满足题意；
当m≠0时，若 的定义域为R，
则 
，
解得m＞1，
综上所述，m＞1
（2）
解： 
= 
，x∈[﹣1，1]，
令 
，则 
，y=t2﹣2at+3，
∵函数y=t2﹣2at+3的图象是开口朝上，且以t=a为对称轴的抛物线，
故当 
时， 
时， 
；
当 
时，t=a时， 
；
当a＞2时，t=2时，h（a）=ymin=7﹣4a．
综上所述，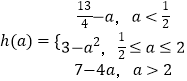 
（3）
解： 
，
假设存在，由题意，知 
解得 
，
∴存在m=0，n=2，使得函数 
的定义域为[0，2]，值域为[0，4]
【解析】（1）若 的定义域为R，则真数大于0恒成立，结合二次函数的图象和性质，分类讨论满足条件的实数m的取值范围，综合讨论结果，可得答案；（2）令 ，则函数y=[f（x）]2﹣2af（x）+3可化为：y=t2﹣2at+3， 
，结合二次函数的图象和性质，分类讨论各种情况下h（a）的表达式，综合讨论结果，可得答案；（3）假设存在，由题意，知 解得答案．
【考点精析】利用二次函数的图象和二次函数的性质对题目进行判断即可得到答案，需要熟知二次函数
的图象是一条抛物线，对称轴方程为
顶点坐标是
；当
时，抛物线开口向上，函数在
上递减，在
上递增；当时，抛物线开口向下，函数在上递增，在上递减．
