题目内容
14.设集合A={a,b},集合B={3,log2(a+3)},若A∩B={0},则A∪B等于( )| A. | {-1,0,3} | B. | {-2,0,3} | C. | {0,3,4} | D. | {1,0,3} |
分析 由已知得log2(a+3)=2,解得a=1,由此求出b=2,从而得到A∪B={1,2,5}.
解答 解:∵集合A={a,b},集合B={3,log2(a+3)},A∩B={0},
∴log2(a+3)=0,解得a=-2,∴b=0,
∴A∪B={-2,0,3}.
故选B
点评 本题考查并集的求法,是基础题,解题时要认真审题,注意交集的性质的合理运用.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
4.某学生对一些对数进行运算,如图表格所示:
现在发觉学生计算中恰好有两次地方出错,那么出错的数据是( )
| x | 0.21 | 0.27 | 1.5 | 2.8 |
| lgx | 2a+b+c-3(1) | 6a-3b-2(2) | 3a-b+c(3) | 1-2a+2b-c(4) |
| x | 3 | 5 | 6 | 7 |
| lgx | 2a-b(5) | a+c(6) | 1+a-b-c(7) | 2(a+c)(8) |
| x | 8 | 9 | 14 | |
| lgx | 3-3a-3c(9) | 4a-2b(10) | 1-a+2b(11) |
| A. | (3),(8) | B. | (4),(11) | C. | (1),(3) | D. | (1),(4) |
9.已知全集U=R,A={x|x<1},B={y|-|x|+y=2},则集合∁U(A∪B)=( )
| A. | {x|1≤x<2} | B. | {x|1<x≤2} | C. | {x|x≥1} | D. | {x|x≤2} |
19.设复数z=$\frac{i}{1-i}$,则z的共轭复数的模等于( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
3.若复数$\frac{a+i}{2i}$的实部和虚部相等,则实数a等于( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
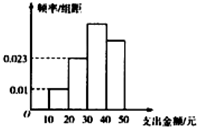 为了解学生在课外活动方面的支出情况,抽取了n个同学进行调查,结果显示这些学生的支出金额(单位:元)都在[10,50],其中支出金额在[30,50]的学生有134人,频率分布直方图如图所示,则n=( )
为了解学生在课外活动方面的支出情况,抽取了n个同学进行调查,结果显示这些学生的支出金额(单位:元)都在[10,50],其中支出金额在[30,50]的学生有134人,频率分布直方图如图所示,则n=( )