题目内容

4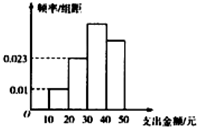．为了解学生在课外活动方面的支出情况，抽取了n个同学进行调查，结果显示这些学生的支出金额（单位：元）都在[10，50]，其中支出金额在[30，50]的学生有134人，频率分布直方图如图所示，则n=（　　）
A．150B．160C．180D．200

分析 先求出支出金额在[10，30]的概率，从而求出支出金额在[30，50]的概率，进而求出答案．

解答 解：由图象得：支出金额在[10，30]的概率是：10×0.01+10×0.23=0.33，
∴支出金额在[30，50]的概率是：1-0.33=0.67，
由134÷0.67=200，得n=200，
故选：D．

点评 本题考察了频率分布直方图问题，考察概率问题，求出支出金额在[30，50]的概率是解题的关键，本题是一道基础题．

练习册系列答案
相关题目
14．设集合A={a，b}，集合B={3，log2（a+3）}，若A∩B={0}，则A∪B等于（　　）
A．{-1，0，3}B．{-2，0，3}C．{0，3，4}D．{1，0，3}
15．对于任意实数x，记[x]表示不超过x的最大整数，{x}=x-[x]，＜x＞表示不小于x的最小整数，若x1，x2，…xm（0≤x1＜x2＜…＜xm≤n+1是区间[0，n+1]中满足方程[x]•{x}•＜x＞=1的一切实数，则x1+x2+…+xm的值是$\frac{n（n+1）}{2}$+$\frac{n}{n+1}$．
12．已知点P在双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）上，F1，F2是这条双曲线上的两个焦点，$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$=0，且△F1PF2的三条边的长度成等差数列，则此双曲线的离心率的值为5．
19．函数f（x）=lnx-$\frac{1}{2}$x2的单调增区间为（　　）
A．（-∞，-1）和（0，1）B．（0，1）C．（-1，0）和（1，+∞）D．（1，+∞）
9．以下5个命题：
①对于相关系r|r|越接近1，则线性相关程度越强；
②空间直角坐标系中，（-2，1，9）关于x轴对称的点的坐标（-2，1，9）；
③某人连续投篮投3次，设事件A：至少有一个命中，事件B：都命中，那么事件A与事件B是互斥且不对立的事件；
④推理“半径为r圆的面积S=πr2，则单位圆的面S=π”是类比推理；
⑤定义运算$[\begin{array}{l}{a}&{c}\\{b}&{d}\end{array}]$$[\begin{array}{l}{x}\\{y}\end{array}]$=$[\begin{array}{l}{ax+cy}\\{bx+dy}\end{array}]$，称$[\begin{array}{l}{x′}\\{y′}\end{array}]$=$[\begin{array}{l}{a}&{c}\\{b}&{d}\end{array}]$$[\begin{array}{l}{x}\\{y}\end{array}]$ 为将点（x，y）映到点（x′，y′）的一次变换．若$[\begin{array}{l}{x′}\\{y′}\end{array}]$=$[\begin{array}{l}{2}&{-1}\\{p}&{q}\end{array}]$$[\begin{array}{l}{x}\\{y}\end{array}]$把直线y=x上的各点映到这点本身，而把直y=3x上的各点映到这点关于原点对称的点，p=3，q=-2；
其中的真命题是①⑤．（写出所有真命题的序号）
16．已知函数 f（x）=ax+（1-a）lnx+$\frac{1}{x}$（a∈R）
（I）当a=0时，求 f（x）的极值；
（Ⅱ）当a＜0时，求 f（x）的单调区间；
（Ⅲ）方程 f（x）=0的根的个数能否达到3，若能请求出此时a的范围，若不能，请说明理由．
13．已知函数f（x）=x3+ax2+bx+c的图象经过原点，且在x=1处取得极大值．
（Ⅰ）求实数a的取值范围；
（Ⅱ）若方程f（x）=-$\frac{{{{（{2a+3}）}^2}}}{9}$恰好有两个不同的根，求f（x）的解析式；
（Ⅲ）对于（2）中的函数f（x），若对于任意实数α和β恒有不等式|f（2sinα）-f（2sinβ）|≤m成立，求m的最小值．
14．直线l的参数方程是$\left\{\begin{array}{l}x=1+2t\\ y=2-t\end{array}\right.\;\;（t∈R）$，则l的方向向量$\overrightarrow d$可以是$（{1，-\frac{1}{2}}）$或（-2，1）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网