题目内容
如图所示,在正方体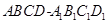 中,E 是
中,E 是 的中点
的中点
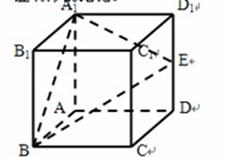
(1)求直线 BE 和平面 所成的角的正弦值,
所成的角的正弦值,
(2)在 上是否存在一点 F,使从
上是否存在一点 F,使从
 平面
平面 ?证明你的结论.
?证明你的结论.
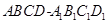 中,E 是
中,E 是 的中点
的中点
(1)求直线 BE 和平面
 所成的角的正弦值,
所成的角的正弦值,(2)在
 上是否存在一点 F,使从
上是否存在一点 F,使从
 平面
平面 ?证明你的结论.
?证明你的结论.(1)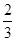 (2)存在,见解析
(2)存在,见解析
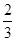 (2)存在,见解析
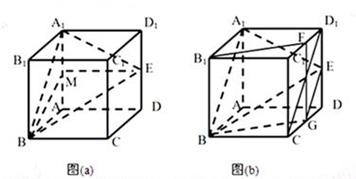
(2)存在,见解析(1)如图(a),取AA1的中点M,连接EM,BM,因为E是DD1的中点,四边形ADD1A1为正方形,所以EM∥AD.
又在正方体ABCD-A1B1C1D1中.AD⊥平面ABB1A1,所以EM⊥面ABB1A1,从而BM为直线BE在平面ABB1A1上的射影,
∠EBM直线BE与平面ABB1A1所成的角.
设正方体的棱长为2,则EM=AD=2,BE=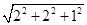 =3,
=3,
于是在Rt△BEM中,sin∠EBM=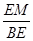 =
=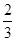
即直线BE与平面ABB1A1所成的角的正弦值为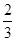
(2)在棱C1D1上存在点F,使B1F平面A1BE,
事实上,如图(b)所示,分别取C1D1和CD的中点F,G,连接EG,BG,CD1,FG,
因A1D1∥B1C1∥BC,且A1D1=BC,所以四边形A1BCD1为平行四边形,
因此D1C∥A1B,又E,G分别为D1D,CD的中点,所以EG∥D1C,从而EG∥A1B,这说明A1,B,G,E共面,所以BG?A1BE
因四边形C1CDD1与B1BCC1皆为正方形,F,G分别为C1D1和CD的中点,所以FG∥C1C∥B1G,且FG=C1C=B1B,因此四边形B1BGF为平行四边形,所以B1F∥BG,而B1F?平面A1BE,BG?平面A1BE,故B1F∥平面A1BE.
又在正方体ABCD-A1B1C1D1中.AD⊥平面ABB1A1,所以EM⊥面ABB1A1,从而BM为直线BE在平面ABB1A1上的射影,
∠EBM直线BE与平面ABB1A1所成的角.
设正方体的棱长为2,则EM=AD=2,BE=
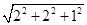 =3,
=3,于是在Rt△BEM中,sin∠EBM=
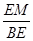 =
=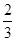
即直线BE与平面ABB1A1所成的角的正弦值为
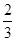
(2)在棱C1D1上存在点F,使B1F平面A1BE,
事实上,如图(b)所示,分别取C1D1和CD的中点F,G,连接EG,BG,CD1,FG,
因A1D1∥B1C1∥BC,且A1D1=BC,所以四边形A1BCD1为平行四边形,
因此D1C∥A1B,又E,G分别为D1D,CD的中点,所以EG∥D1C,从而EG∥A1B,这说明A1,B,G,E共面,所以BG?A1BE
因四边形C1CDD1与B1BCC1皆为正方形,F,G分别为C1D1和CD的中点,所以FG∥C1C∥B1G,且FG=C1C=B1B,因此四边形B1BGF为平行四边形,所以B1F∥BG,而B1F?平面A1BE,BG?平面A1BE,故B1F∥平面A1BE.


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 、
、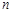 是两条不同的直线,
是两条不同的直线,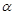 、
、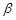 是两个不同的平面,则下列命题中真命题是
是两个不同的平面,则下列命题中真命题是

 ∥
∥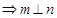
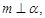
 、
、 、
、 、
、 是空间四个不同的点,在下列命题中,不正确的是( )
是空间四个不同的点,在下列命题中,不正确的是( ) 与
与 共面,则
共面,则 与
与 共面
共面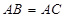 ,
, ,则
,则

 的底面
的底面 是边长为4的正方形,
是边长为4的正方形, ,
,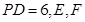 分别为
分别为 中点。
中点。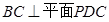 。
。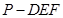 的体积。
的体积。
 中,
中,  的中点为
的中点为 ,
, 的中点为
的中点为 ,则异
,则异 与
与 所成的是( )
所成的是( )




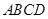 为平行四边形,
为平行四边形,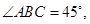
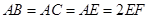 ,
,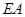 ⊥平面
⊥平面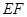 ∥
∥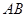 ,
,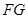 ∥
∥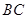 ,
,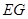 ∥
∥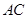 .
.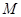 是线段
是线段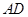 的中点,求证:
的中点,求证: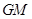 ∥平面
∥平面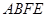 ;
;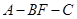 的余弦值.
的余弦值.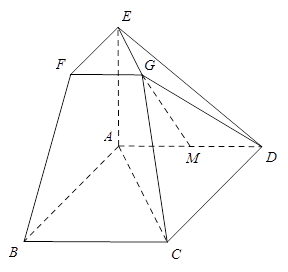
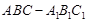 中,
中,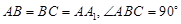 ,点
,点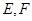 分别是棱
分别是棱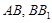 的中点,则异面直线
的中点,则异面直线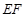 和
和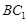 所成角是( )度
所成角是( )度