题目内容
设 、
、 、
、 、
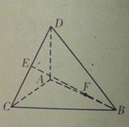
、 是空间四个不同的点,在下列命题中,不正确的是( )
是空间四个不同的点,在下列命题中,不正确的是( )
 、
、 、
、 、
、 是空间四个不同的点,在下列命题中,不正确的是( )
是空间四个不同的点,在下列命题中,不正确的是( )A.若 与 与 共面,则 共面,则 与 与 共面 共面 |
B.若 与 与 是异面直线,则 是异面直线,则 与 与 是异面直线 是异面直线 |
C.若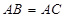 , , ,则 ,则 |
D.若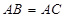 , , ,则 ,则 |
C
因为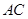 与
与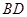 共面,所以
共面,所以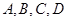 四点共面,所以
四点共面,所以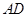 与
与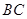 共面,命题A正确;
共面,命题A正确;
若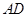 与
与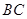 共面,则由上面的证明可知
共面,则由上面的证明可知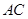 与
与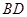 共面,与
共面,与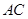 与
与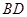 异面矛盾,所以
异面矛盾,所以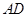 与
与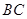 异面,命题B正确;
异面,命题B正确;
若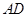 与
与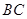 共面,因为
共面,因为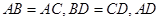 为公共边,所以
为公共边,所以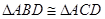 ,则
,则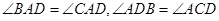 ,即
,即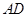 是
是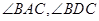 平分线。而
平分线。而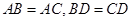 ,所以有
,所以有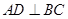 。若
。若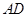 与
与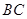 异面,则取
异面,则取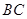 中点
中点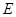 ,连接
,连接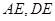 。由
。由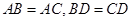 可得
可得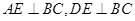 ,所以
,所以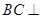 面
面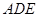 ,从而有
,从而有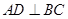 。综上可得,
。综上可得,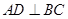 成立,命题D正确;
成立,命题D正确;
当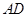 与
与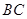 共面时,若四边形
共面时,若四边形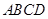 是普通四边形时,可以有
是普通四边形时,可以有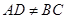 ,命题C不正确,故选C
,命题C不正确,故选C
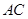 与
与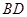 共面,所以
共面,所以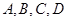 四点共面,所以
四点共面,所以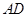 与
与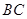 共面,命题A正确;
共面,命题A正确;若
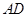 与
与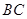 共面,则由上面的证明可知
共面,则由上面的证明可知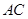 与
与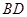 共面,与
共面,与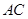 与
与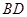 异面矛盾,所以
异面矛盾,所以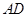 与
与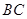 异面,命题B正确;
异面,命题B正确;若
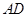 与
与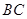 共面,因为
共面,因为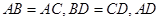 为公共边,所以
为公共边,所以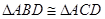 ,则
,则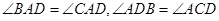 ,即
,即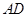 是
是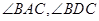 平分线。而
平分线。而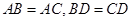 ,所以有
,所以有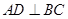 。若
。若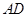 与
与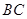 异面,则取
异面,则取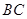 中点
中点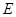 ,连接
,连接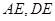 。由
。由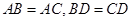 可得
可得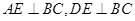 ,所以
,所以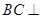 面
面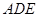 ,从而有
,从而有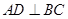 。综上可得,
。综上可得,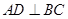 成立,命题D正确;
成立,命题D正确;当
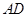 与
与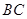 共面时,若四边形
共面时,若四边形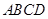 是普通四边形时,可以有
是普通四边形时,可以有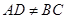 ,命题C不正确,故选C
,命题C不正确,故选C
练习册系列答案
相关题目
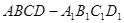 的棱长为2,E为AB的中点.
的棱长为2,E为AB的中点.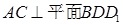
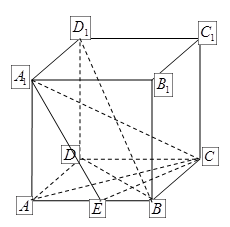
 中,E 是
中,E 是 的中点
的中点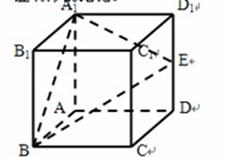
 所成的角的正弦值,
所成的角的正弦值, 上是否存在一点 F,使从
上是否存在一点 F,使从
 平面
平面 ?证明你的结论.
?证明你的结论.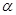 是空间中的一个平面,
是空间中的一个平面,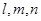 是三条不同的直线,则下列命题中正确的是( )
是三条不同的直线,则下列命题中正确的是( ) ;
;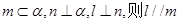 ;
; ,则
,则

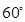 的二面角,连结PC、PD,在AD上取一点E使得3AE=ED,连结PE得到如下图(图2)的一个几何体.
的二面角,连结PC、PD,在AD上取一点E使得3AE=ED,连结PE得到如下图(图2)的一个几何体.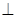 平面PCD;
平面PCD;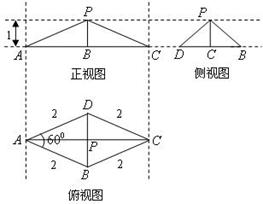
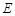 在何处时,
在何处时,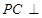 面EBD,并求出此时二面角
面EBD,并求出此时二面角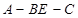 平面角的余弦值.
平面角的余弦值.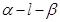 的大小为
的大小为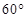 ,点
,点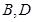 棱
棱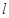 上,
上,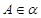 ,
,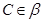 ,
,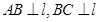 ,
,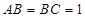 ,
,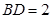 ,则异面直线
,则异面直线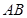 与
与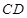 所成角的余弦值为
所成角的余弦值为



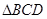 的( )
的( ) 平面ABC,
平面ABC, ,AC=CB=AD=2,E是DC的中点,F是AB的中点。
,AC=CB=AD=2,E是DC的中点,F是AB的中点。 ;
;