题目内容
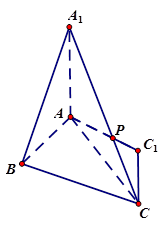
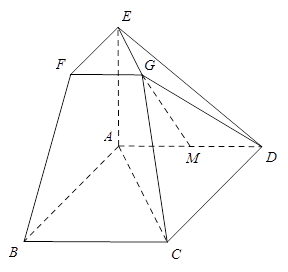
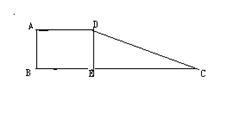
在如图所示的几何体中,四边形 为平行四边形,
为平行四边形,
 ,
,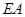 ⊥平面
⊥平面 ,
, ∥
∥ ,
,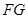 ∥
∥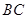 ,
,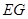 ∥
∥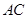 .
.
(1)若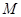 是线段
是线段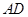 的中点,求证:
的中点,求证: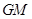 ∥平面
∥平面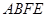 ;
;
(2)求二面角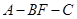 的余弦值.
的余弦值.
 为平行四边形,
为平行四边形,
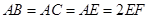 ,
,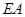 ⊥平面
⊥平面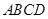 ,
,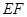 ∥
∥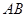 ,
,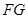 ∥
∥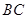 ,
,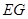 ∥
∥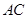 .
.(1)若
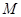 是线段
是线段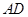 的中点,求证:
的中点,求证: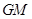 ∥平面
∥平面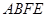 ;
;(2)求二面角
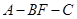 的余弦值.
的余弦值.
证:因为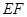 ∥
∥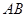 ,
,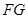 ∥
∥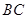 ,
,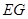 ∥
∥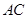 .所以
.所以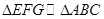 .
.
由于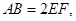 因此
因此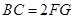 .
.
连接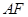 ,
, .
.
在平 行四边形
行四边形 中,M是线段AD的中点,
中,M是线段AD的中点,
则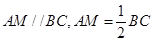 ,
,
因此,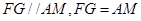 ,所以四边形AFGM为平行四边形,
,所以四边形AFGM为平行四边形,
所以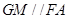 ,
,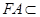 平面
平面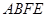 ,
,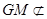 平面
平面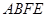 ,
,
所以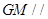 平面
平面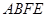 .……5分
.……5分
(2)分别以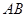 ,
,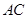 ,
,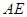 所在直线为
所在直线为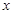 轴,
轴, 轴,
轴,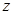 轴建立空间直角坐标系,
轴建立空间直角坐标系,
不妨设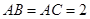 ,则由题意得
,则由题意得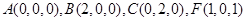
平面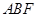 的法向量为
的法向量为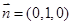 ,平面
,平面 的法向量为
的法向量为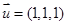
则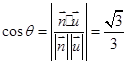 .……10分
.……10分
 ∥
∥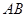 ,
,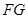 ∥
∥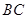 ,
,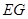 ∥
∥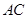 .所以
.所以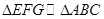 .
.由于
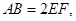 因此
因此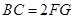 .
.连接
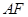 ,
,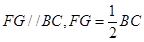 .
.在平
 行四边形
行四边形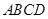 中,M是线段AD的中点,
中,M是线段AD的中点,则
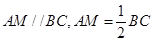 ,
,因此,
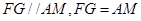 ,所以四边形AFGM为平行四边形,
,所以四边形AFGM为平行四边形,所以
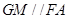 ,
,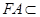 平面
平面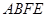 ,
,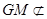 平面
平面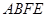 ,
,所以
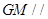 平面
平面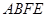 .……5分
.……5分(2)分别以
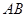 ,
,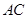 ,
,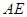 所在直线为
所在直线为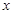 轴,
轴, 轴,
轴,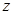 轴建立空间直角坐标系,
轴建立空间直角坐标系,不妨设
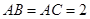 ,则由题意得
,则由题意得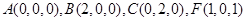
平面
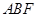 的法向量为
的法向量为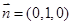 ,平面
,平面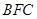 的法向量为
的法向量为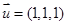
则
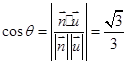 .……10分
.……10分略

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
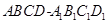 中,E 是
中,E 是 的中点
的中点
 所成的角的正弦值,
所成的角的正弦值, 上是否存在一点 F,使从
上是否存在一点 F,使从
 平面
平面 ?证明你的结论.
?证明你的结论.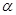 是空间中的一个平面,
是空间中的一个平面,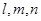 是三条不同的直线,则下列命题中正确的是( )
是三条不同的直线,则下列命题中正确的是( ) ;
;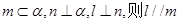 ;
; ,则
,则

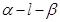 的大小为
的大小为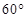 ,点
,点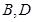 棱
棱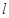 上,
上,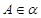 ,
,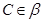 ,
,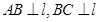 ,
,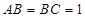 ,
,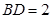 ,则异面直线
,则异面直线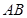 与
与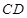 所成角的余弦值为
所成角的余弦值为



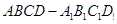 中,
中,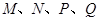 分别是
分别是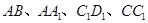 的中点,给出以下四个结论:
的中点,给出以下四个结论: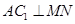 ; ②
; ②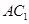 //平面
//平面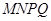 ; ③
; ③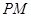 相交; ④
相交; ④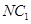 与
与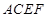 的边
的边 与正方形
与正方形 所在平面垂直,
所在平面垂直,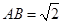 ,
,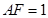 ,
,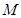 是线段
是线段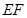 的中点。
的中点。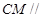 平面
平面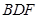 ;
;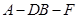 的大小。
的大小。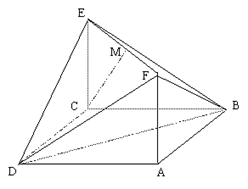
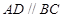 ,
,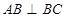 ,
,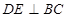 ,
,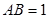 ,
,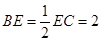 ,以DE为轴旋转至图(2)位置,F为DC的中点.
,以DE为轴旋转至图(2)位置,F为DC的中点. 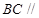 平面
平面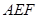
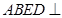 平面
平面 ,且BC垂直于AE
,且BC垂直于AE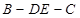 的大小.
的大小.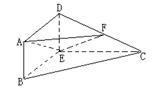
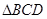 的( )
的( )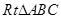 中,
中,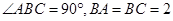 ,分别过
,分别过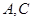 作平面
作平面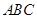 的垂线
的垂线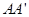 和
和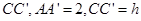 ,连结
,连结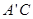 和
和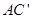 交于点
交于点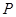 .
.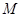 为
为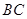 中点,若
中点,若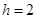 ,求证:直线
,求证:直线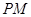 与平面
与平面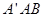 平行;
平行;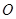 为
为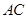
 中点,二面角
中点,二面角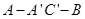 等于
等于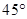 ,求直线
,求直线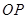 与平面
与平面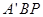 所成角
所成角