Question

【题目】已知函数f（x）=eax（a≠0）．
（1）当 时，令 （x＞0），求函数g（x）在[m，m+1]（m＞0）上的最小值；
（2）若对于一切x∈R，f（x）﹣x﹣1≥0恒成立，求a的取值集合；
（3）求证： ．

Answer 1

【答案】
（1）解：当a= 时，g（x）= ，则g'（x）= ．

当 ﹣1＞0，即x＞2时，g'（x）＞0；

当 ﹣1＜0且x≠0，即x＜2或0＜x＜2时，g'（x）＜0．

则g（x）的增区间为（2，+∞），减区间为（﹣∞，0），（0，2）．

因为m＞0，所以m+1＞1，

①当m+1≤2，即0＜m≤1时，g（x）在[m，m+1]上单调递减，

所以g（x）min=g（m+1）=

②当m＜2＜m+1，即1＜m＜2时，g（x）在[m，2]上单调递减，

在[2，m+1]上单调递增，所以g（x）min=g（2）=

③当m≥2时，g（x）在[m，m+1]上单调递增，所以g（x）min=g（m）= ．

综上，g（x）min=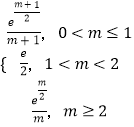

（2）解：设h（x）=f（x）﹣x﹣1=eax﹣x﹣1

若a＜0，则对一切x＞0，h（x）＜0这与题设矛盾．

又a≠0，故a＞0．而h'（x）=aeax﹣1，令h'（x）=0，得x= ，

当x＜ 时，h'（x）＜0，h（x）单调递减；

当x＞ 时，h'（x）＞0，h（x）单调递增．

故当x= 时，h（x）取最小值 ﹣ ﹣1．

于是对一切x∈R，h（x）≥0恒成立，当且仅当 ﹣1≥0①

令φ（x）=t﹣tlnt﹣1，则φ'（x）=﹣lnt

当0＜t＜1时，φ'（t）＞0，φ（t）单调递增；

当t＞1时，φ'（t）＜0，φ（t）单调递减，

故当t=1时，φ（t）取最大值φ（1）=0，

因此，当且仅当 =1，即a=1时，①式成立．

综上所述，a的取值集合为{1}

（3）证明：由（2）可知，当x＞0时，g（x）= ，

所以 （x＞0），

可得 ≤

于是 +

≤

＜

= ＜

【解析】（1）求出函数的导数，解关于导函数的表达式，求出函数的单调区间，通过讨论m的范围求出函数的最小值即可；（2）设h（x）=f（x）﹣x﹣1=eax﹣x﹣1，求出a＞0，解根据导函数的不等式，求出函数的单调区间，得到当且仅当 ﹣1≥0①令φ（x）=t﹣tlnt﹣1，根据函数的单调性求出a的范围即可；（3）由g（x）= ，可得 ≤ ，根据不等式的性质证明即可．