题目内容
【题目】在平面直角坐标系xoy中,以O为极点,x轴的正半轴为极轴的极坐标系中,直线l的极坐标方程为θ= ![]() ,曲线C的参数方程为
,曲线C的参数方程为 ![]() .
.
(1)写出直线l与曲线C的直角坐标方程;
(2)过点M平行于直线l1的直线与曲线C交于A、B两点,若|MA||MB|= ![]() ,求点M轨迹的直角坐标方程.
,求点M轨迹的直角坐标方程.
【答案】
(1)解:直线l的极坐标方程为θ= ![]() ,所以直线斜率为1,直线l:y=x;
,所以直线斜率为1,直线l:y=x;
曲线C的参数方程为 ![]() .消去参数θ,
.消去参数θ,
可得曲线 ![]()
(2)解:设点M(x0,y0)及过点M的直线为 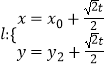
由直线l1与曲线C相交可得: ![]()
![]() ,即:
,即: ![]() ,
,
x2+2y2=6表示一椭圆
取y=x+m代入 ![]() 得:3x2+4mx+2m2﹣2=0
得:3x2+4mx+2m2﹣2=0
由△≥0得 ![]()
故点M的轨迹是椭圆x2+2y2=6夹在平行直线 ![]() 之间的两段弧
之间的两段弧
【解析】(1)利用极坐标与直角坐标方程的互化,直接写出直线l的普通方程,消去参数可得曲线C的直角坐标方程;(2)设点M(x0 , y0)以及平行于直线l1的直线参数方程,直线l1与曲线C联立方程组,通过|MA||MB|= ![]() ,即可求点M轨迹的直角坐标方程.通过两个交点推出轨迹方程的范围,
,即可求点M轨迹的直角坐标方程.通过两个交点推出轨迹方程的范围,

练习册系列答案
相关题目
