题目内容
【题目】已知在平面四边形ABCD中，AB= 
，BC=2，AC⊥CD，AC=CD，则四边形ABCD面积的最大值为 ．
【答案】3+ 
【解析】解：如图所示，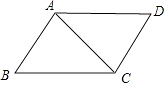 
设∠ABC=θ，θ∈（0，π），
则在△ABC中，由余弦定理得，
AC2=AB2+BC2﹣2ABBCcosθ=6﹣4 
cosθ；
∴四边形ABCD的面积为
S=S△ABC+S△ACD
= 
（ABBCsinθ+ACCD），
化简得
S= （2 sinθ+6﹣4 cosθ）
=3+ （sinθ﹣2cosθ）
=3+ sin（θ﹣φ），
其中tanφ=2，
当sin（θ﹣φ）=1时，
S取得最大值为3+ ．
故答案为：3+ ．
设∠ABC=θ，θ∈（0，π），由余弦定理求出AC2 ， 再求四边形ABCD的面积表达式，利用三角恒等变换求出它的最大值．
备战中考寒假系列答案
【题目】某社区超市购进了A，B，C，D四种新产品，为了解新产品的销售情况，该超市随机调查了15位顾客（记为ai ， i=1，2，3，…，15）购买这四种新产品的情况，记录如下（单位：件）：
顾 | a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 | a11 | a12 | a13 | a14 | a15 |
A | 1 | 1 | 1 | 1 | 1 | ||||||||||
B | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||||||
C | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||
D | 1 | 1 | 1 | 1 | 1 | 1 |
（Ⅰ）若该超市每天的客流量约为300人次，一个月按30天计算，试估计产品A的月销售量（单位：件）；
（Ⅱ）为推广新产品，超市向购买两种以上（含两种）新产品的顾客赠送2元电子红包．现有甲、乙、丙三人在该超市购物，记他们获得的电子红包的总金额为X，求随机变量X的分布列和数学期望；
（Ⅲ）若某顾客已选中产品B，为提高超市销售业绩，应该向其推荐哪种新产品？（结果不需要证明）
【题目】某学校高一、高二、高三三个年级共有300名教师，为调查他们的备课时间情况，通过分层抽样获得了20名教师一周的备课时间，数据如下表（单位：小时）：
高一年级 | 7 | 7.5 | 8 | 8.5 | 9 | |||
高二年级 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
高三年级 | 6 | 6.5 | 7 | 8.5 | 11 | 13.5 | 17 | 18.5 |
（1）试估计该校高三年级的教师人数；
（2）从高一年级和高二年级抽出的教师中，各随机选取一人，高一年级选出的人记为甲，高二年级选出的人记为乙，假设所有教师的备课时间相对独立，求该周甲的备课时间不比乙的备课时间长的概率；
（3）再从高一、高二、高三三个年级中各随机抽取一名教师，他们该周的备课时间分别是8、9、10（单位：小时），这三个数据与表格中的数据构成的新样本的平均数记为 
，表格中的数据平均数记为 
，试判断 与 的大小．（结论不要求证明）
