Question

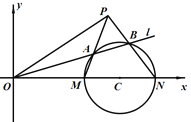
【题目】为建设美丽乡村，政府欲将一块长12百米，宽5百米的矩形空地ABCD建成生态休闲园，园区内有一景观湖EFG（图中阴影部分），以AB所在直线为x轴，AB的垂直平分线为y轴，建立平面直角坐标系xOy（如图所示）．景观湖的边界线符合函数y=x+ （x＞0）模型，园区服务中心P在x轴正半轴上，PO= 百米．
（1）若在点O和景观湖边界曲线上一点M之间修建一条休闲长廊OM，求OM的最短长度；
（2）若在线段DE上设置一园区出口Q，试确定Q的位置，使通道PQ最短．

Answer 1

【答案】
（1）解：设M（x，x+ ），则|OM|2=x2+（x+ ）2=2x2+ +2≥2 +2，

当且仅当2x2= 即x2= 时取等号，

∴|OM|的最短距离为

（2）解：过P作函数y=x+ 的切线l，设切线l的方程为y=k（x﹣ ）（k＜0），

联立方程组 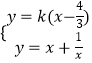，得（1﹣k）x2+ x+1=0，

令△= k2﹣4（1﹣k）=0得k=﹣3或k= （舍），

∴直线l的方程为y=﹣3（x﹣ ），

令y=5得x=﹣ ，

∴DQ=6﹣ = ．

∴当|DQ|= 时，通道PQ最短

【解析】（1）设M（x，x+ ），利用距离公式得出|OM|2关于x的函数，利用基本不等式求出最小值即可；（2）当直线PQ与湖边界相切时，通道最短，设出切线方程，与边界函数联立，令△=0即可得出切线方程，从而确定Q点的位置．